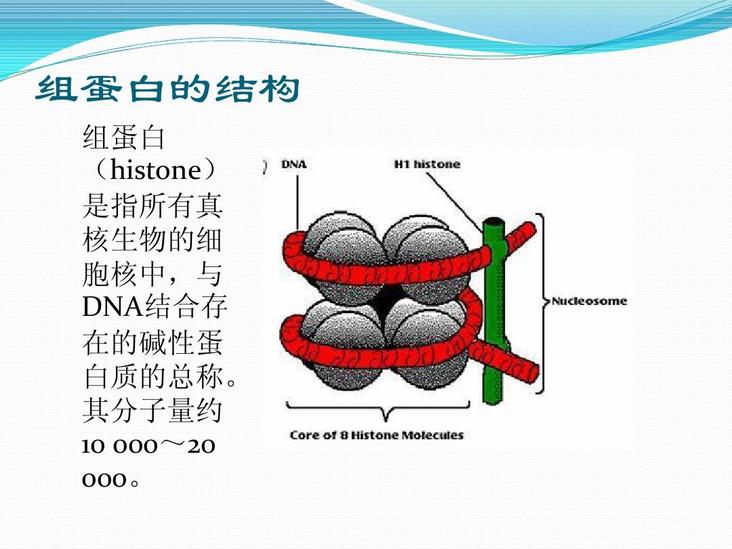组蛋白本词条是多义词，共2个义项德国A.科塞尔发现的蛋白质组蛋白是真核生物染色体的基本结构蛋白，是真核生物体细胞染色质中的碱性蛋白质，含精氨酸和赖氨酸等碱性氨基酸特别多，二者加起来约为所有氨基酸残基的1/4。

拉奥本词条是多义词，共2个义项印度固体化学家拉奥（C.N.R.Rao），印度国籍，固体化学家，1934年6月生于印度班加罗尔。现任印度贾瓦哈拉尔?尼赫鲁先进科技研究中心荣誉主任。印度科学院(IAS)和印度国家科学院(INSA)院士。1958年获得美国普渡大学博士学位。2013年当选中国科学院外籍院士。拉奥的主要研究领域是固态和材料化学、结构化学，该领域是化学科学的重要分支，也是化学科学与物理、材料

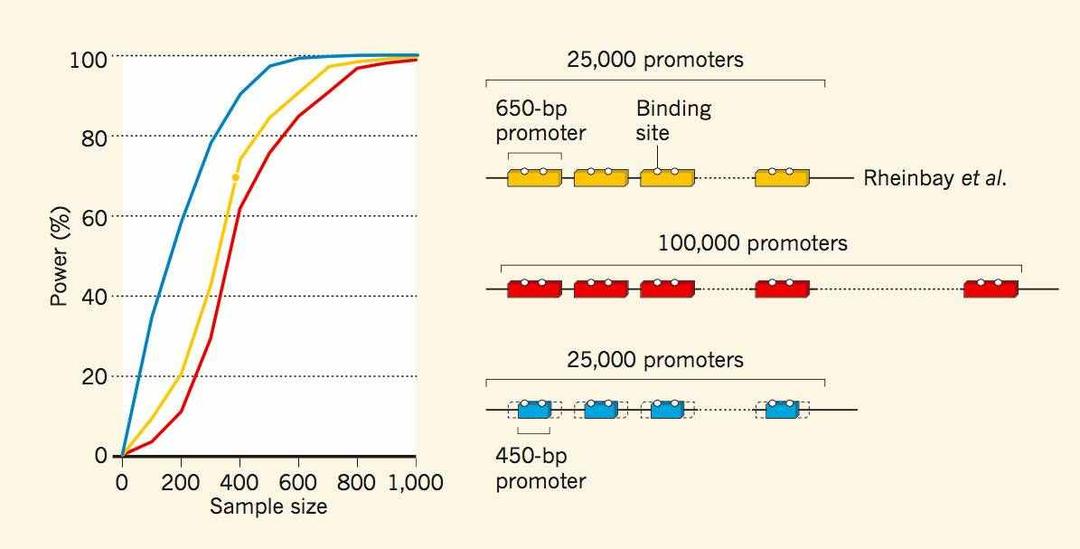编码区生物学专用术语基因在结构上，分为编码区和非编码区两部分（其中非编码区对基因的表达主要起调控作用，如启动子等位于该区）。真核生物基因的编码区是不连续的，分为外显子和内含子（其中外显子是可以最终实现表达（表现在蛋白质的一级结构上），内含子则最终不能表达（所以真核生物基因表达过程中，转录产物——信使RNA不能直接进行翻译，而是要修剪掉内含子部分后才能去指导翻译）。原核生物的基因是连续的，所以谈不上

超几何函数数学领域中的函数超几何函数，作为超几何方程的解，通过无限项的多项式（即幂级数）定义的函数，其系数按特定的规则确定。

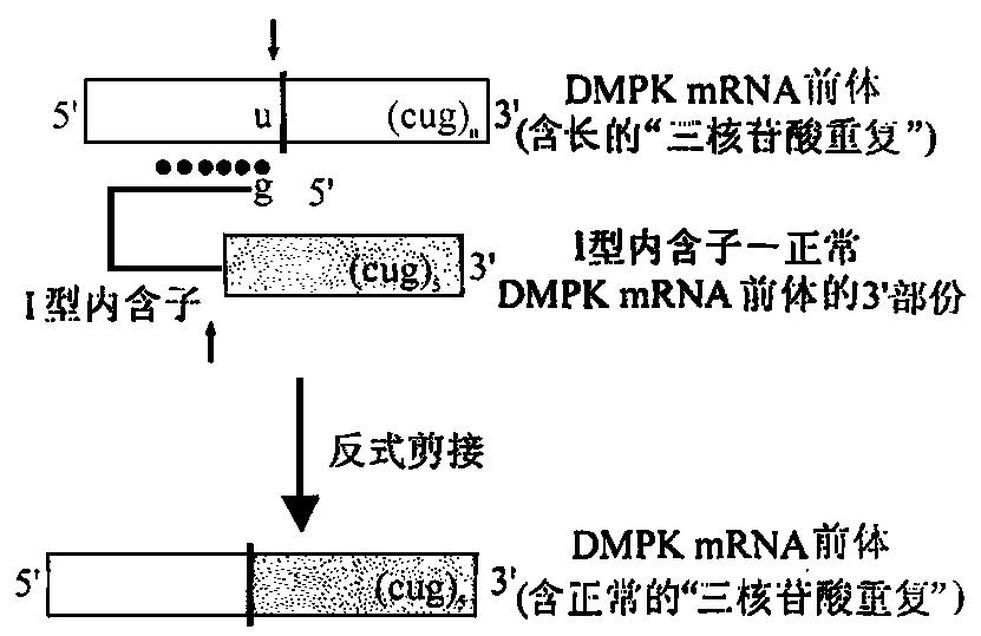反式剪接反式剪接 指的是两条不同的pre-mRNA的外显子连接到一起。与正常的顺式剪接不同，这里的两段外显子是来自不同的pre-mRNA的，但却可能来自同一基因。“经典”反式剪接见于锥虫和线虫，近期在人类身上也发现了反式剪接。

皮埃尔·德利涅比利时科学家、数学家1988年获得克拉福德奖皮埃尔·勒内·德利涅子爵（法语：Vicomte Pierre René Deligne，1944年10月3日－），生于布鲁塞尔，比利时数学家。他最重要的贡献之一是20世纪70年代关于韦伊猜想的工作。

插入片段将一段DNA序列载入到细菌质粒中，这一段被整合的序列被称为插入片段。

菲尔兹奖数学领域的国际最高奖项之一菲尔兹奖（Fields Medal），是据加拿大数学家约翰·查尔斯·菲尔兹（John Charles Fields）要求设立的国际性数学奖项，于1936年首次颁发，常被视为数学界的诺贝尔奖（诺贝尔奖本身未设数学奖）。菲尔兹奖每四年颁奖一次，在由国际数学联盟（IMU）主办的四年一度的国际数学家大会（ICM）上举行颁奖仪式，每次颁给二至四名有卓越贡献的年轻数学家。获奖

纯粹数学专门研究数学本身规律的学科纯粹数学也叫基础数学，是一门专门研究数学本身，不以实际应用为目的的学问，研究从客观世界中抽象出来的数学规律的内在联系，也可以说是研究数学本身的规律。相对于应用数学而言，和其它一些不以应用为目的的理论科学(例如理论物理、理论化学)有密切的关系。纯粹数学以其严格、抽象和美丽着称。自18世纪以来，纯粹数学成为数学研究的一个特定种类，并随着探险、天文学、物理学、工程学等的

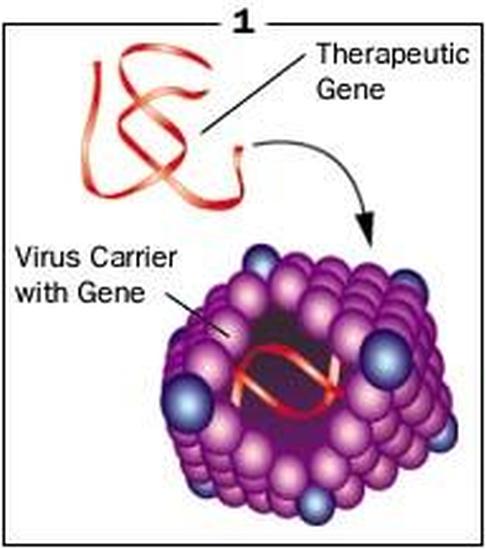反转录病毒RNA病毒之一逆转录病毒（Retrovirus），又称反转录病毒，属于RNA病毒中的一类，它们的遗传信息不是储存在脱氧核糖核酸（DNA），而是储存在核糖核酸（RNA）上，此类病毒是目前已知的唯一基因组不是单倍体的病毒。逆转录病毒基因组为二倍体，两条相同的单股正链RNA，其两端为长末端重复序列（LTR），具有启动子、增强子功能，对病毒DNA的转录调控具有重要作用。病毒核心包含逆转录酶和整合

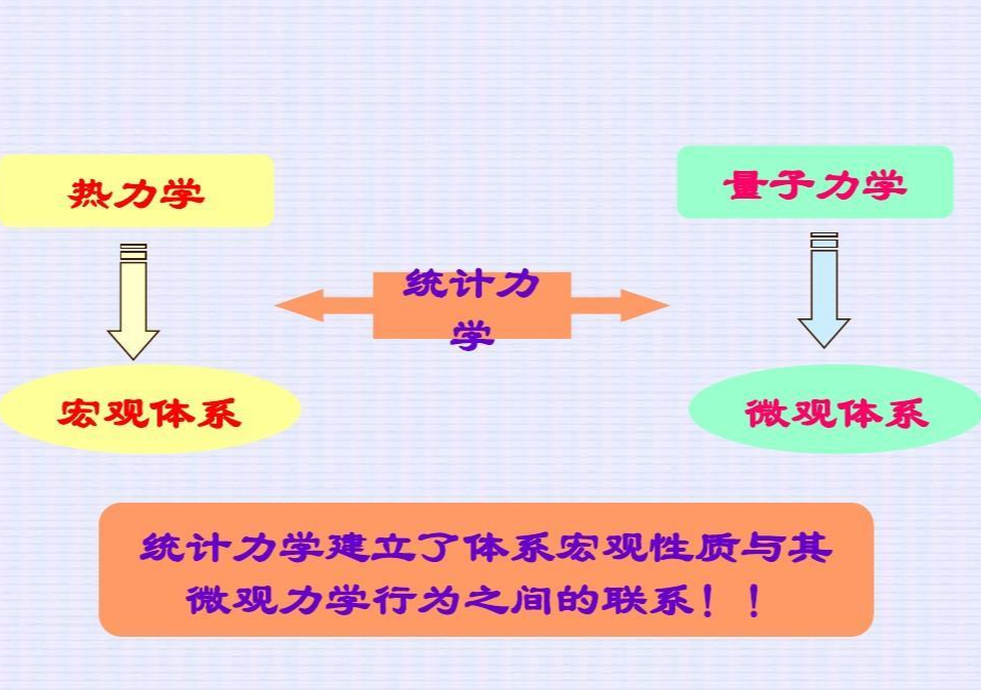统计力学本词条是多义词，共3个义项物理学概念统计力学（又叫统计物理学）是研究大量粒子（原子、分子）集合的宏观运动规律的科学。统计力学运用的是经典力学原理。由于粒子的量大，存在大量的自由度，虽然和经典力学应用同样的力学规律，但导致性质上完全不同的规律性。不服从纯粹力学的描述，而服从统计规律性，用量子力学方法进行计算，得出和用经典力学方法计算相似的结果。从这个角度来看，统计力学的正确名称应为统计物理学

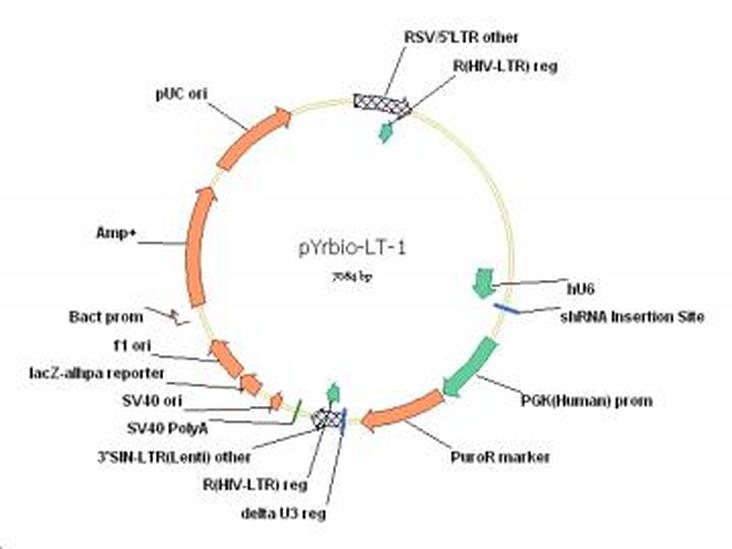穿梭载体穿梭载体(shuttle vector) 是指能在两种不同的生物中复制的载体，含有不止一个ori、能携带插入序列在不同种类宿主中繁殖，在原核生物和真核细胞中都能复制和表达。这类载体不仅具有细菌质粒的复制原点及选择标记基因，还有真核生物的自主复制序列(ARS) 以及选择标记性状，具有多克隆位点。通常穿梭载体在细菌中用于克隆，扩增克隆的基因在酵母菌中用于基因表达分析。

测温学测温学是一种涉及温度，热流，温度等相关物理量的测量科学。基本信息性质测量科学基本简介测温学热学计量是涉及温度，热流，温度等相关物理量的测量科学，依据热力学定律建立热学计量标准，开展各种测量仪表的鉴定好校准，实现中低温，高温，光电高温，辐射温度和热流，温度

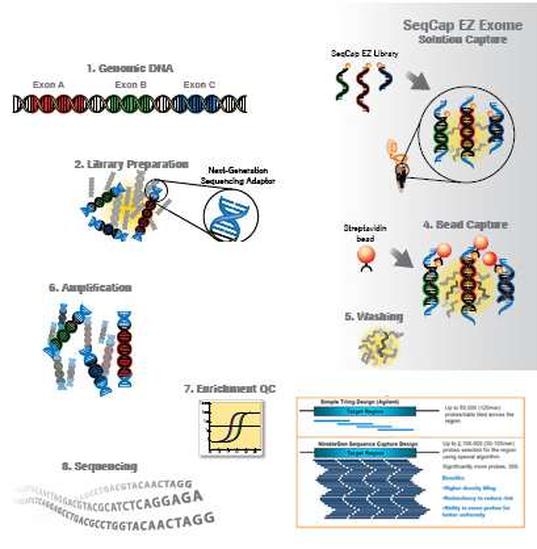外显子捕获外显子捕获外显子捕获(exon trapping) 是构建一种载体，从其插入片段中识别和回收外显子序列，从而克隆目的基因。捕获外显子的载体pETV—SD是一种反转录病毒穿梭载体，即可在不同种生物中如大肠杆菌和酵母，细菌和哺乳动物细胞等进行复制的载体因为凡是有内含子和外显子的基因在转录后都要经过RNA剪接，这就需要有剪接供体(splicing donor，SD)位点和剪接受体(splici

孤立波本词条是多义词，共2个义项孤立波有限振幅波的一种，只有一个波峰或波谷，而且只出现在浅水水域中。

戴维·希尔伯特德国著名数学家近代形式公理学派的创始人戴维·希尔伯特，又译大卫·希尔伯特，（DavidHilbert，1862-1943），德国著名数学家。他于1900年8月8日在巴黎第二届国际数学家大会上，提出了新世纪数学家应当努力解决的23个数学问题，被认为是20世纪数学的至高点，对这些问题的研究有力推动了20世纪数学的发展，在世界上产生了深远的影响。希尔伯特领导的数学学派是19世纪末20世纪初

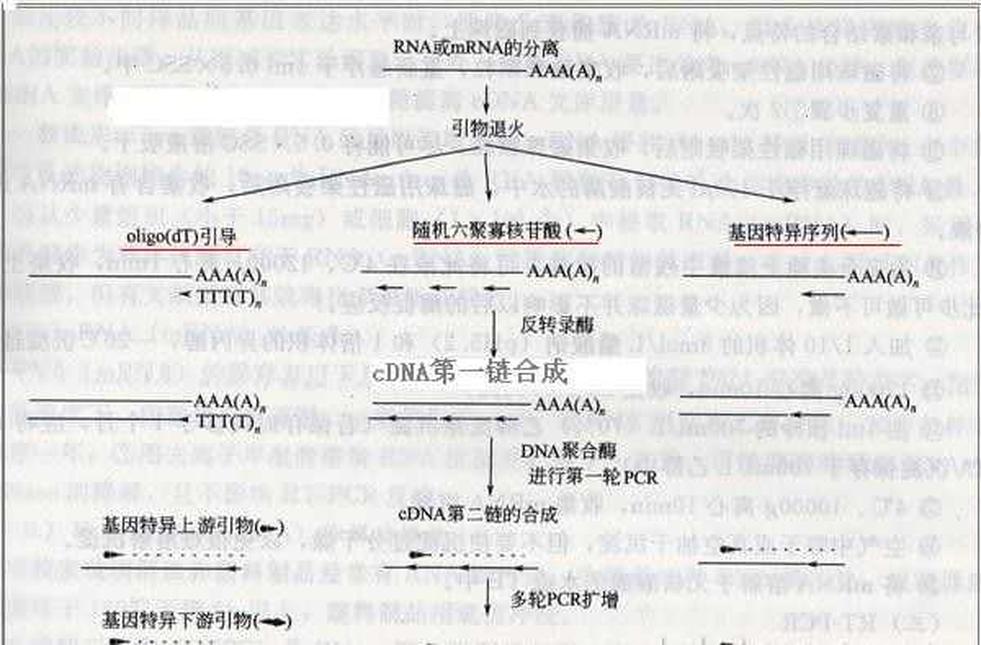反转录DNA生物合成的特殊方式反转录是以RNA为模板，通过反转录酶，合成DNA的过程。是DNA生物合成的一种特殊方式。反转录是进行基因工程过程中，以RNA为模板提取出DNA遗传信息的过程。

拉宾德拉纳特•泰戈尔（Rabindranath Tagore，1861年5月7日-1941年8月6日），是19-20世纪印度诗人、文学家、社会活动家、哲学家以及印度民族主义者，以诗集、小说及剧本闻名。他第一位获得诺贝尔文学奖的亚洲人，一生共创作50余部诗集，30余部散文，12部中篇、长篇小说，近百部短篇小说，20多个剧本，2000多幅绘画，包括印度国歌在内的2000余首歌曲及大量散文，少部分游记、

附加体附加体（episome）：在细胞中或以游离态、或以与染色体相结合的状态存在着的遗传结构。

史宇光本词条是多义词，共2个义项北京大学数学科学学院教授史宇光，北京大学数学科学学院教授、副院长。2007年获得国家杰出青年基金项目资助。2009年获得第十一届中国青年科技奖。2011年当选长江讲座教授。2011年获得拉马努金奖。

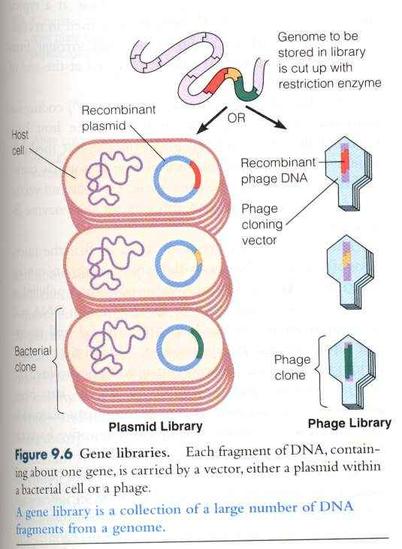基因文库全部基因组序列的集合体基因文库包括基因组文库和部分基因文库。将含有某种生物不同基因的许多DNA片段，导入受体菌的群体中储存，各个受体菌分别含有这种生物的不同的基因，称为基因文库。如果这个文库包含了某种生物的所有基因，那么，这种基因文库叫做基因组文库。如果这个文库只包含了某种生物的一部分基因，这种基因文库叫做部分基因文库，例如cDNA文库，首先得到mRNA，再反转录得cDNA，形成文库。cD

恽之玮麻省理工学院数学教授恽之玮，1982年11月2日出生于江苏常州，数学家，麻省理工学院数学教授。1989年-1995年，常州市局前街小学，获第五届华罗庚金杯少年数学邀请赛复赛一等奖。1995年-2000年，江苏省常州高级中学，获第四十一届国际数学奥林匹克金牌（满分）。2000年-2004年，北京大学数学科学学院数学与应用数学专业本科，获理学士学位。2004年-2009年，普林斯顿大学数学系研究

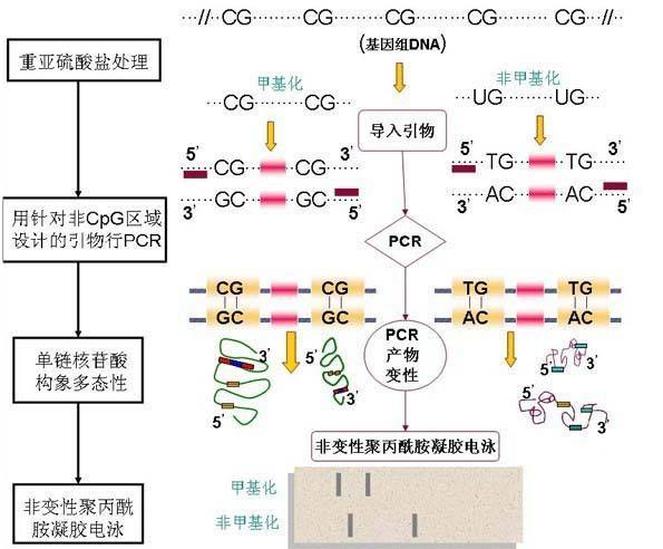单链构象多态性单链构象多态性（single-strand conformation polymorphism，SSCP）是一种分离核酸的技术，可以分离相同长度但序列不同的核酸（性质类似于DGGE和TGGE，但方法不同）。

数学期刊数学期干IJ(mathematical periodicals)数学专业刊物。它是传播、交流数学科学学术思想，并及时反映数学科学研究成果的有力工具。它的出现是数学科学事业发展的需要，反过来又有力地促进了数学事业的发展。

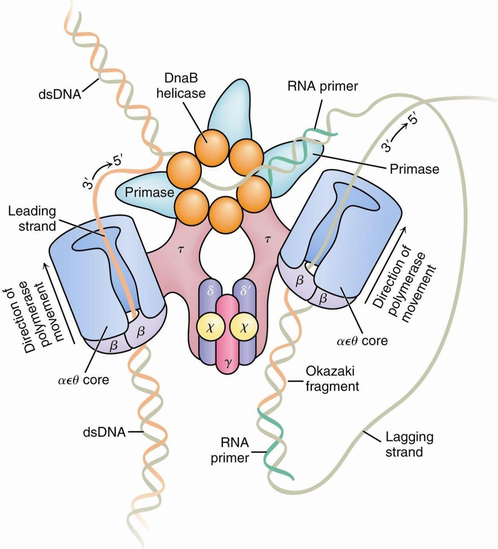聚合酶1957年美国发现的物质聚合酶（polymerase）又称多聚酶。是专门生物催化合成脱氧核糖核酸(DNA)和核糖核酸(RNA)的一类酶的统称。1957年，美国科学家阿瑟·科恩伯格（Arthur Kornberg）发现。