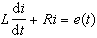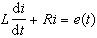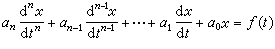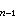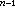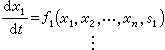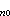电路的稳定性（电路的稳定性）

正文

动态电路在运行中受到各种扰动而不引起工作状态的质的变化，或扰动消失后能返回(或接近于)原来的工作状态的性质。稳定是电路能正常工作的必要条件。稳定性问题涉及电路中电流、电压的变化，因此它只在动态电路（含电感、电容等元件的电路）里才出现。而实际电路一定存在电感（例如导线的电感）、电容（如导体间的电容），它们都是动态电路，因而总存在稳定性问题。

线性定常电路的稳定性　线性定常 n阶电路的电路方程是常系数n阶常微分方程。例如电阻R、电感L串联电路的电路方程是一阶常微分方程：

电路的稳定性

式中i是电流,e（t）是作用于电路的电动势。一般讲来，电路方程的形式如下：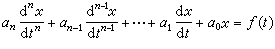

电路的稳定性

式中f(t)由独立电源决定，而且│f(t)│＜M，M是一个确定的正数；系数a0,a1，…，an是常数。上述微分方程的特征方程是

anPn＋a

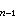
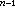
电路的稳定性

＋…a1P＋a0＝0

这个特征方程是n个根P1，P2,…，Pn,称作特征值。如果所有特征值的实部小于零，则微分方程的解χ 的绝对值不会无限增长，对应的电路是稳定的。如果有任何一个特征值的实部大于零，则解χ的绝对值会无限增长，对应的电路是不稳定的。例如上述一阶电路的特征方程是LP＋R＝0,只有一个特征值 P1＝-R/L。当R＞0、L＞0时，P1＜0,电路稳定。一般讲来，由电阻、电感、电容（它们都是正常数）和独立电源构成的电路，是稳定的电路。如果电路中含有放大器或含有受控电源时，电路可能不稳定。

非线性电路的稳定性问题　许多非线性电路的电路方程可用状态方程描述：

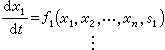
电路的稳定性

式中χ1，…，χn是状态变量，通常代表电感、电流和电容、电压；s1，…，sn是由独立电源决定的量，若电源是直流电源，它们是常量，否则它们是时间t的函数。指定状态变量χ1，χ2，…之值，决定了n维状态空间中的一点。χi是时间函数时，状态量的变化由状态空间里点随时间运动的轨线表示。

不变解的稳定性　直流电源作用于电路时，电路方程可有不变解，它代表电路中各处的电压、电流是不随时间变化的常量。这时所有状态变量也是常量，记作χ10，χ20，…,χ

电路的稳定性

,由状态空间中一个不动的点P代表。该点称不动点或平衡点（图1）。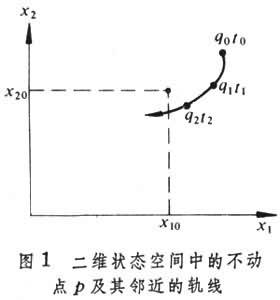

电路的稳定性

由于某种干扰，在t0时刻状态稍许偏离了不动点P而位于P点周围任一点q0，从t0时刻开始，由q0发出的轨线如图1曲线所示，曲线上q1、q2分别代表t1、t2时点的位置。若对于任何时刻ti,由不动点P到qi的距离di总是很小，不动点P是稳定的，即电路不变解是稳定的。若qi最终趋于P点，不动点P是渐近稳定的，这代表虽然干扰使状态偏离不变解，但最后状态会回到该不变解。若qi最终远离P点，不动点是不稳定的。

直流电源作用下，非线性电路的不变解可以不止一个，与之对应的状态方程的不动点可以不止一个。只有那些渐近稳定的不动点才和电路的稳态解对应。

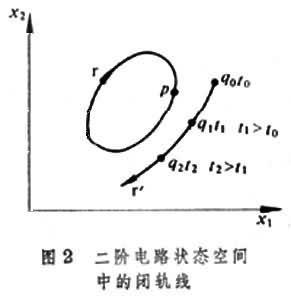
电路周期解的稳定性　电路的周期解用状态变量表示时是χ1＝φ1(t),χ2＝φ2(t)，…，χn＝φn(t)，所有φi(t)函数是t的周期函数，周期为T。在状态空间里，点的轨线是一条闭曲线。图2所示为二阶电路状态空间中的闭轨线r。

电路的稳定性

设t0时，点P的坐标是χ1=φ1(t0)、χ2＝φ2(t0)。经过一个周期，即在t0＋T时刻，状态点仍位于P点。设由于某种干扰,t0时刻的状态稍许离开 P点而是位于 P点周围的任一点q0。从t0开始，从q0发出的轨线如图2中曲线r┡所示，图中,q1、q2代表t1、t2时的点的位置。若r┡最终趋于闭轨线r,称周期解是稳定的；若r┡远离r,称周期解是不稳定的。只有稳定的周期解，才是电路的稳态解。

结构稳定性　电路的响应和电路参数有关。电阻、电感、电容、正弦电源的振幅和频率等，都是电路参数。由于各种干扰，这些参数不能维持为固定不变的值，总会有微小变化。若参数的微小变化，能引起电路响应的质的变化，则在该参数下的电路称为结构不稳定的电路，反之称为结构稳定的电路。例如设 RLC串联电路中的电阻R的绝对值丨R丨极小。若R＞0，电路中的电压、电流的波形是衰减振荡波形，电路是稳定的；若R＜0,波形是增幅振荡波形，电路是不稳定的。这两种波形有质的不同。R＝0称作参数R的分岔值。在分岔值的两侧，电路响应有质的变化。R＝0时的电路就是结构不稳定的。R≠0时的电路是结构稳定的。设某个带反馈的放大电路可以将信号放大。增大放大器的放大倍数β,若它超过某个分岔值β0时，电路中激起振荡。放大倍数为临界值时的放大电路，是结构不稳定的；而β≠β0时的电路是结构稳定电路。电路参数刚好是分岔值的概率是零，因此实际电路总是结构稳定电路。但研究结构不稳定电路，对于了解电路性质的变化是有意义的。