二次函数（quadratic function）的基本表示形式为y=ax²+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。

二次函数表达式为y=ax²+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。

如果令y值等于零，则可得一个二次方程。该方程的解称为方程的根或函数的零点。

中文名

二次函数

外文名

Quadratic function

拼音

èr cì hán shù

术语类别

数学术语

顶点坐标

（h，k）

函数图像

抛物线

对称轴

直线x=h

两根式

y=a(x-x1)(x-x2)

常用作图方法

五点法

函数表达式

y=ax²+bx+c（a≠0 abc为常数)

顶点式

y=a(x-h)²+k

学科

数学

基本定义

一般地，把形如

（a、b、c是常数）的函数叫做二次函数，其中a称为二次项系数，b为一次项系数，c为常数项。x为自变量，y为因变量。等号右边自变量的最高次数是2。

函数图像顶点坐标

交点式

为

（

仅限于与x轴有交点的抛物线

），

与x轴的交点坐标是

和

。

注意

：“变量”不同于“自变量”，不能说“二次函数是指变量的最高次数为二次的多项式函数”。“未知数”只是一个数（具体值未知，但是只取一个值），“变量”可在实数范围内任意取值。在方程中适用“未知数”的概念（函数方程、微分方程中是未知函数，但不论是未知数还是未知函数，

一般都表示一个数或函数

——也会遇到特殊情况），但是函数中的字母表示的是变量，意义已经有所不同。从函数的定义也可看出二者的差别，如同函数不等于函数的关系。

历史

大约在公元前480年，古巴比伦人和中国人已经使用配方法求得了二次方程的正根，但是并没有提出通用的求解方法。公元前300年左右，欧几里得提出了一种更抽象的几何方法求解二次方程。

7世纪印度的婆罗摩笈多是第一位懂得使用代数方程的人，它同时容许有正负数的根。

11世纪阿拉伯的花拉子密独立地发展了一套公式以求方程的正数解。亚伯拉罕·巴希亚（亦以拉丁文名字萨瓦索达著称）在他的著作Liber embadorum中，首次将完整的一元二次方程解法传入欧洲。

据说施里德哈勒是最早给出二次方程的普适解法的数学家之一。但这一点在他的时代存在着争议。这个求解规则是：在方程的两边同时乘以二次项未知数的系数的四倍；在方程的两边同时加上一次项未知数的系数的平方；然后在方程的两边同时开二次方（引自婆什迦罗第二）。

函数性质

对于二次函数的一般形式

，有如下性质：

1.

二次函数的图像是抛物线，但抛物线不一定是二次函数。开口向上或者向下的抛物线才是二次函数。抛物线是轴对称图形。对称轴为直线

。对称轴与抛物线唯一的交点为抛物线的顶点P。特别地，当b=0时，抛物线的

对称轴是y轴

（即直线x=0）。

2.

二次函数图像有一个顶点P，坐标为P

。当

时，P在y轴上；当

时，P在x轴上。

3.

二次项系数a决定抛物线的开口方向和大小。

当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。|a|越大，则抛物线的开口越小

；

|a|越小，则抛物线的开口越大。

4.

一次项系数b和二次项系数a共同决定对称轴的位置。

当a与b同号时（即ab>0），对称轴在y轴左侧；当a与b异号时（即ab<0），对称轴在y轴右侧。

（可巧记为：左同右异）

5.

常数项c决定抛物线与y轴交点。抛物线与y轴交于(0, c）。

6.

抛物线与x轴交点个数：

时，抛物线与x轴有2个交点。

时，抛物线与x轴有1个交点。当

时，抛物线与x轴没有交点。

7.

当

时，函数在

取得最小值

；在

上是减函数，在

上是增函数；抛物线的开口向上；函数的值域是

。

当

时，函数在

处取得大值

；在

上是增函数，在

上是减函数；抛物线的开口向下；函数的值域是

。

当

时，抛物线的对称轴是y轴，这时，函数是偶函数，解析式变形为

。

8.

定义域：R

9.值域：

当a>0时，值域是

；当a<0时，值域是

。

10.

奇偶性

：

当b=0时，此函数是偶函数；当b不等于0时，此函数是非奇非偶函数。

11.周期性：

无

表达式

顶点式

(a≠0,a、h、k为常数),顶点坐标为（h,k)

，

对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数

的图像相同，当x=h时，y最大（小）值=k。有时题目会指出让你用配方法把一般式化成顶点式。

例：

已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。

解：

设

，把(3,10)代入上式，解得

。

注意：

与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。

具体可分为下面几种情况：

当h>0时，y=a(x-h)²的图像可由抛物线y=ax²向右平行移动h个单位得到；

当h<0时，y=a(x-h)²的图像可由抛物线y=ax²向左平行移动|h|个单位得到；

当h>0,k>0时，将抛物线y=ax²向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)²+k的图象；

当h>0,k<0时，将抛物线y=ax²向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)²+k的图象；

当h<0,k>0时，将抛物线y=ax²向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)²+k的图象；

当h<0,k<0时，将抛物线y=ax²向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)²+k的图象。

交点式

(仅限于与x轴即y=0有交点时的抛物线，即b-4ac≥0)。

已知抛物线与x轴即y=0有交点A(x1, 0)和B(x2, 0)，我们可设

，然后把第三点代入x、y中便可求出a。

由一般式变为交点式的步骤：

(韦达定理)

重要概念：

a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；a<0时，开口方向向下。a的绝对值可以决定开口大小。a的绝对值越大开口就越小，a的绝对值越小开口就越大。

由此可引导出交点式的系数

(y为截距)　二次函数表达式的右边通常为

二次

三项式。

欧拉

交点式：

若

有两个实根

,

，则

此抛物线的对称轴为直线

。三点式

方法1：

已知二次函数上三个点，

、

、

。把三个点分别代入函数解析式

(a≠0,a、h、k为常数)，有：

得出一个三元一次方程组，就能解出a、b、c的值。

方法2：

已知二次函数上三个点，

、

、

利用拉格朗日插值法，可以求出该二次函数的解析式为：

与X轴交点的情况：

当

时，函数图像与x轴有两个交点，分别是

和

。

当

时，函数图像与x轴只有一个切点，即

。

当

时，抛物线与x轴没有公共交点。x的取值范围是虚数（

）

函数图像

基本图像

在平面直角坐标系中作出二次函数y=ax+bx+c的图像，可以看出，在没有特定定义域的二次函数图像是一条永无止境的抛物线。如果所画图形准确无误，那么二次函数图像将是由

平移得到的。轴对称

二次函数图像是

轴对称

图形。对称轴为直线

对称轴与二次函数图像

唯一

的交点为二次函数图象的顶点P。

特别地，当b=0时，二次函数图像的对称轴是

y轴

（即直线x=0）。是顶点的横坐标（即x=0）。

a,b同号，对称轴在y轴左侧；

a,b异号，对称轴在y轴右侧。

顶点

二次函数图像有一个顶点P，坐标为P(h,k)。

当h=0时，P在y轴上；当k=0时，P在

x轴

上。即可表示为顶点式y=a(x-h)+k（x≠0）

,

。开口

二次项系数a决定二次函数图像的开口方向和大小。当

a>0

时，二次函数图象

向上

开口；当

a<0

时，二次函数图像

向下

开口。

越大

，则二次函数图像的开口

越小

。位置决定因素

一次项系数b和二次项系数a共同决定对称轴的位置。

当a>0,与b

同

号时（即ab

>

0），对称轴在

y轴左

；因为对称轴在左边则对称轴

小于

0，也就是

,所以

要大于0，所以a、b要同号

当a>0,与b

异

号时（即ab

<

0），对称轴在

y轴右

。因为对称轴在右边则对称轴要

大于

0，也就是

, 所以

要小于0，所以a、b要异号

可简单记忆为

左同右异

，即当对称轴在y轴左时，a与b同号（即a>0，b>0或a<0，b<0）；当对称轴在y轴右时，a与b异号（即a0或a>0，b<0）（ab<0）。

事实上，b有其自身的几何意义：二次函数图象与y轴的交点处的该二次函数图像切线的函数解析式（一次函数）的斜率k的值。可通过对二次函数求导得到。

交点决定因素

常数项c决定二次函数图像与y轴交点。

二次函数图像与y轴交于（0,C）点

注意：顶点坐标为（h,k)，与y轴交于（0,C)。

与x轴交点数

对于函数y=a(x-h)+k，交点个数如下：

a<0；k>0或a>0；k<0时，二次函数图像与x轴有2个交点。

k=0时，二次函数图像与x轴只有1个交点。

质疑点：a<0；k<0或a>0，k>0时，二次函数图像与x轴无交点。

当a>0时，函数在x=h处取得最小值

，在xh范围内是增函数（即y随x的变大而变大），二次函数图像的开口向上，函数的值域是y>k

当a<0时，函数在x=h处取得最大值

，在xh范围内是减函数（即y随x的变大而变小），二次函数图像的开口向下，函数的值域是y当h=0时，抛物线的对称轴是y轴，这时，函数是偶函数。

对称关系

对于

一般式：

①y=ax+bx+c与y=ax-bx+c两图像关于y轴对称

②y=ax+bx+c与y=-ax-bx-c两图像关于x轴对称

③y=ax+bx+c与y=-ax+bx+c-b/2a关于顶点对称

④y=ax+bx+c与y=-ax+bx-c关于原点中心对称。（即绕原点旋转180度后得到的图形）

对于顶点式：

①y=a(x-h)+k与y=a(x+h)+k两图像关于y轴对称，即顶点(h, k)和(-h, k)关于y轴对称，横坐标相反、纵坐标相同。

②y=a(x-h)+k与y=-a(x-h)-k两图像关于x轴对称，即顶点(h, k)和(h, -k)关于x轴对称，横坐标相同、纵坐标相反。

③y=a(x-h)+k与y=-a(x-h)+k关于顶点对称，即顶点(h, k)和(h, k)相同，开口方向相反。

④y=a(x-h)+k与y=-a(x+h)-k关于原点对称，即顶点(h, k)和(-h, -k)关于原点对称，横坐标、纵坐标都相反。

（其实①③④就是对

f(x)

来说f(-x),-f(x),-f(-x)的情况

）

图像画法

五点法

五点草图法又被叫做五点作图法是二次函数中一种常用的作图方法。

注明：虽说是草图，但画出来绝不是草图。

五点草图法中的五个点都是极其重要的五个点，分别为：顶点、与x轴的交点、与y轴的交点及其关于对称轴的对称点。

Ps.正规考试也是用这种方法初步确定图像。但是正规考试的要求在于要列表格，取x、y，再确定总体图像。五点法是可以用在正规考试中的。

描点法

在初中数学中，要求采用描点法画出二次函数图像。

其做法与五点法类似：【以

为例】

1、列表

x……-1-0.50122.53……

……73.51-113.57……

先取顶点，用虚线画出对称轴。取与x轴两个交点（如果存在）、y轴交点及其对称点（如果存在）和另外两点及其对称点。

Ps.原则上相邻x的差值相等，但远离顶点的点可以适当减小差值

2、依据表格数据绘制函数图像，如图

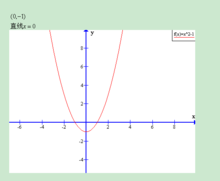
方程关系

特别地，二次函数（以下称函数）

,

当y=0时，二次函数为关于x的一元二次方程（以下称方程），即

此时，函数图像与x轴有无交点即方程有无实数根。

函数与x轴交点的横坐标即为方程的根。

1．二次函数

，

，

，

(各式中，a≠0)的图象形状相同，只是位置不同，它们的顶点坐标及对称轴如下表：

(0，0) x=0

(0，K) x=0

(h，0) x=h

(h，k) x=h

y=ax²+bx+c

，

当h>0时，

的图象可由抛物线y=ax²向右平行移动h个单位得到，

当h<0时，则向左平行移动|h|个单位得到。

当h>0,k>0时，将抛物线

向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)²+k（h>0,k>0）的图象

当h>0,k<0时，将抛物线

向右平行移动h个单位，再向下移动|k|个单位，就可得到y=a(x-h)²+k（h>0,k<0）的图象

当h<0,k>0时，将抛物线

向左平行移动|h|个单位，再向上移动k个单位，就可得到y=a(x+h)²+k（h<0,k>0）的图象

当h<0,k<0时，将抛物线

向左平行移动|h|个单位，再向下移动|k|个单位，就可得到y=a(x+h)²+k（h<0,k<0）的图象

在向上或向下。向左或向右平移抛物线时，可以简记为“上加下减，左加右减”。

因此，研究抛物线

(a≠0)的图像，通过配方，将一般式化为

的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了。这给画图像提供了方便。

2．抛物线

(a≠0)的图像：当a>0时，开口向上，当a<0时开口向下，对称轴是直线

，顶点坐标是

。

3．抛物线

(a≠0)，若a>0，当

时，y随x的增大而减小；当

时，y随x的增大而增大。若a<0，当

时，y随x的增大而增大；当

时，y随x的增大而减小。

4．抛物线

的图像与坐标轴的交点：

(1)图像与y轴一定相交，交点坐标为(0, c)；

(2)当

时，图像与x轴交于两点

和

，其中的

,

是一元二次方程

(a≠0)的两根．这两点之间的距离

另外，抛物线上任何一对对称点的距离可以由

（A为其中一点的横坐标的两倍）

当

时，图像与x轴只有一个切点；

当

时，图像与x轴没没有共。当a>0时，图像落在x轴的上方，x为任何实数时，都有y>0；当a<0时，图像落在x轴的下方，x为任何实数时，都有y<0。

5．抛物线

的最值：如果a>0，则当

时，

；如果a<0，则当

时，

。

顶点的横坐标，是取得最值时的自变量值，顶点的纵坐标，是最值的取值。

6．用待定系数法求二次函数的解析式

(1)当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时，可设解析式（表达式）为一般形式：

(2)当题给条件为已知图像的顶点坐标或对称轴或极大（小）值时，可设解析式为顶点式：

(a≠0)。

(3)当题给条件为已知图像与x轴的两个交点坐标时，可设解析式为两根式：

(a≠0)。

学习方法

知识要点

1.要理解函数的意义。

2.要记住函数的几个表达形式，注意区分。

3.一般式，顶点式，交点式，等，区分对称轴，顶点，图像，y随着x的增大而减小（增大）(增减值）等的差异性。

4.联系实际对函数图象的理解。

5.计算时，看图像时切记取值范围。

6.随图象理解数字的变化而变化。二次函数考点及例题

二次函数知识很容易与其他知识综合应用，而形成较为复杂的综合题目。因此，以二次函数知识为主的综合性题目是中考的热点考题，往往以大题形式出现。

误区提醒

（1）对二次函数概念理解有误，漏掉二次项系数不为0这一限制条件；

（2）对二次函数图像和性质存在思维误区；

（3）忽略二次函数自变量取值范围；

（4）平移抛物线时，弄反方向

。

定义与表达式152次播放02:55二次函数和二次方程由什么联系和区别？

一般地，自变量x和因变量y之间存在如下关系：

（a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下，IaI还可以决定开口大小，IaI越大开口就越小，IaI越小开口就越大.）

则称y为x的二次函数。

二次函数表达式的右边通常为二次三项式。

三种表达式

一般式：

（a，b，c为常数，a≠0）

顶点式：y=

[抛物线的顶点P(h, k)]

交点式：

[仅限于与x轴有交点

和

的抛物线]

注：在3种形式的互相转化中，有如下关系：

，

，

抛物线的性质2095次播放01:29【二次函数】 17 二次函数的图像变换

1.抛物线是轴对称图形。对称轴为直线

。

对称轴与抛物线唯一的交点为抛物线的顶点P。

特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）

2.抛物线有一个顶

点P，坐标为

当

时，P在y轴上；当

时，P在x轴上。

3.二次项系数a决定抛物线的开口方向，|a|决定抛物线开口大小。

当a>0时，抛物线开口向上；当a<0时，抛物线开口向下

|a|越大，则抛物线的开口越小。

4.一次项系数b和二次项系数a有1个交点。

5.常数项c决定抛物线与y轴交点。抛物线与y轴交于（0，c）

抛物线与x轴

交点个数

>0时，抛物线与x轴有2个交点。

=0时，抛物线与x轴有1个交点。

<0时，抛物线与x轴没有交点。系数表达的意义

a.决定抛物线的开口方向和大小。当a>0时，抛物线向上开口；当a<0时，抛物线向下开口。

b.和a共同决定对称轴的位置。当a与b同号时（即ab>0），对称轴在y轴左；当a与b异号时（即ab<0），对称轴在y轴右。

c.决定抛物线与y轴交点。抛物线与y轴交于（0,c）