设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶矩阵B,使得:AB=BA=E。则我们称B是A的逆矩阵,而A则被称为可逆矩阵。 注:E为单位矩阵。
逆矩阵相关的文章
郭芙是金庸小说《射雕英雄传》和《神雕侠侣》中的角色。她是郭靖和黄蓉的长女,也是东邪黄药师的外孙女,桃花岛的第三代继承人。她和杨过从小就相识,并一起成长。郭芙受到外公黄药师的珍视,得到父亲郭靖的信任,与黄蓉母女关系深厚,被称为"芙蓉"。她出生在桃花岛,儿童时期随父母到嘉兴,曾救助过武氏兄弟和杨过等人。
鼻炎是一种常见的鼻腔黏膜炎症性疾病。多发生于春夏交替的季节,我国发病率呈上升的趋势。病因较为复杂,与多种因素有关,病毒感染是首要原因。主要表现为鼻塞、鼻痒、打喷嚏、流鼻涕、嗅觉下降、头痛、头昏等。主要通过药物治疗来缓解症状,此外还会有变应原特异性免疫治疗、手术治疗等。如未及时治疗,可能会引起急性鼻窦
麦芽糖是一种由两个葡萄糖分子以α-1,4糖苷键连接而成的淀粉糖产品,也称为麦芽二糖。根据麦芽糖含量的不同,麦芽糖浆可分为普通麦芽糖浆、高麦芽糖浆和超高麦芽糖浆。麦芽糖是一种碳水化合物,由含淀粉酶的麦芽作用于淀粉而制得,可用作营养剂和培养基的配制。此外,麦芽糖也是一种中国传统怀旧小食。
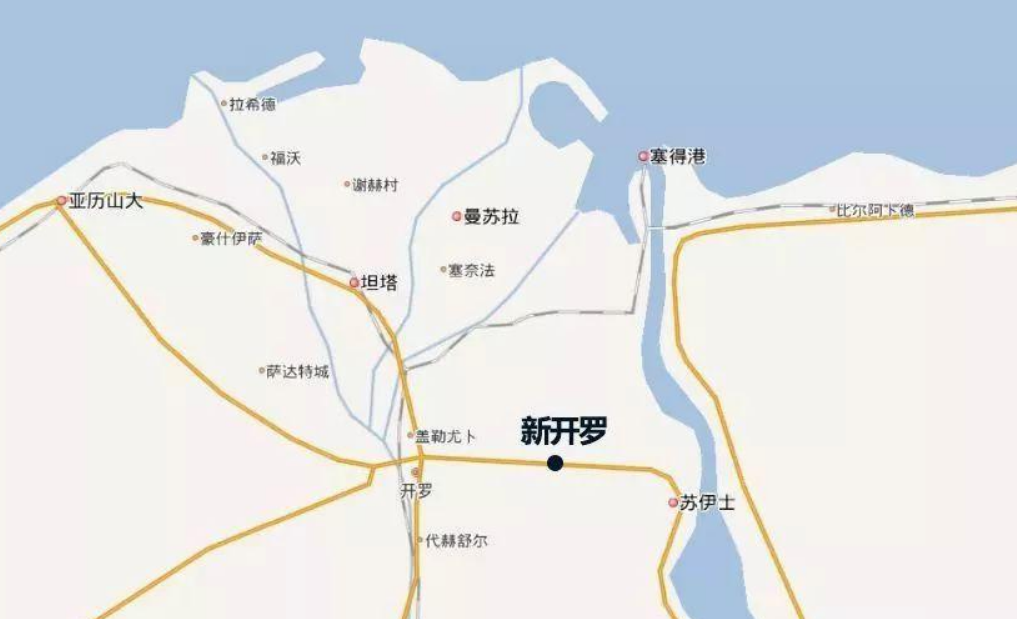
新开罗”将是一个人为创造出来的首都,可能与现在的埃及格格不入,却符合政治精英们对埃及未来的幻想。计划中的“新开罗”将是一个美丽的地方,一个“创新中心”,具有可持续发展的环境,城市居民享有高质量的生活,人们在这里可以自由呼吸,而不会因沙尘暴咳嗽不已。与之相比,“老开罗”是一个丑陋的城市。从机场到市区,一路上的建筑物都被污染物弄得脏兮兮的。耳朵里充斥着刺耳的汽车笛声,一到冬天,尼罗河上就笼罩着一层浓雾。街道上总是塞满了汽车,它们就像是这座城市的动脉血栓一样。当然,尼罗河畔会有些时尚女士穿着高跟鞋踱步,让这个城
19~20世纪初阿富汗人民抗击英国入侵、维护民族独立的战争。亦称英阿战争。阿富汗是18世纪中叶形成的多民族的大地主和封建贵族专政的伊斯兰国家,战略地位重要,是19世纪英、俄争夺的对象之一。沙俄视阿富汗为其南下印度洋的战略跳板,英国则视阿富汗为维护英属印度北方统治的屏障。阿富汗依靠各部族武装和广大人民的支持,胜利地抗击了英军的入侵。

尚可名片
这家伙太懒了,什么都没写!