-
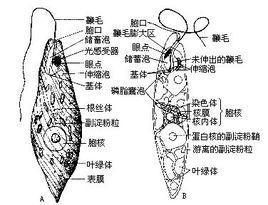 隐鞭虫属03-03隐鞭虫属(Cryptobia),是一种生物学学科的一种专有名词。是原生动物门、鞭毛虫纲、动基体目、波豆科的一属。体呈叶状,具有2根鞭毛,一根朝前,游离,另一根部分地贴近虫体,但不形成典型的波动膜。主要种类:本属在我国淡水鱼已有十多种的记录。
隐鞭虫属03-03隐鞭虫属(Cryptobia),是一种生物学学科的一种专有名词。是原生动物门、鞭毛虫纲、动基体目、波豆科的一属。体呈叶状,具有2根鞭毛,一根朝前,游离,另一根部分地贴近虫体,但不形成典型的波动膜。主要种类:本属在我国淡水鱼已有十多种的记录。 -

-
 等积投影网03-03
等积投影网03-03 -

-
 鱼波豆虫属03-03鱼波豆虫属(Ichthyobodo)虫体呈梨形或卵形。具纵口沟,在其前端着生有2根(有时4根)向后游离的鞭毛。胞核1个,圆形。寄生于淡水鱼类的体表和鳃部。1928在我国分布很广泛,可造成鱼病。它寄生于多种淡水鱼类。全国主要养鱼区均有分布。
鱼波豆虫属03-03鱼波豆虫属(Ichthyobodo)虫体呈梨形或卵形。具纵口沟,在其前端着生有2根(有时4根)向后游离的鞭毛。胞核1个,圆形。寄生于淡水鱼类的体表和鳃部。1928在我国分布很广泛,可造成鱼病。它寄生于多种淡水鱼类。全国主要养鱼区均有分布。 -

-

-
 巴尔的摩事件03-031986年4月,特里萨·嘉莉与戴维·巴尔的摩等人在《细胞》杂志合作发表了一篇论文.后来,特里萨·嘉莉的同事玛格特·欧图勒提出论文数据有造假嫌疑 .此事由于关联到巴尔的摩,而他有巨大的学术影响力,并且其极力为特里萨·嘉莉辩护而引起了巨大的社会反响.中文史称巴尔的摩事件,英文史称特里萨·嘉莉事件(Imanishi-Kari case) .1991年,美国国立卫生研究院(NIH)调查小组的报告泄露后,巴尔的摩被迫辞去洛克菲勒大学校长职务 .1996年,NIH的另一个独立调查小组推翻了该调查小组对嘉莉的全部19项
巴尔的摩事件03-031986年4月,特里萨·嘉莉与戴维·巴尔的摩等人在《细胞》杂志合作发表了一篇论文.后来,特里萨·嘉莉的同事玛格特·欧图勒提出论文数据有造假嫌疑 .此事由于关联到巴尔的摩,而他有巨大的学术影响力,并且其极力为特里萨·嘉莉辩护而引起了巨大的社会反响.中文史称巴尔的摩事件,英文史称特里萨·嘉莉事件(Imanishi-Kari case) .1991年,美国国立卫生研究院(NIH)调查小组的报告泄露后,巴尔的摩被迫辞去洛克菲勒大学校长职务 .1996年,NIH的另一个独立调查小组推翻了该调查小组对嘉莉的全部19项 -
 浙江乌岩岭昆虫及其森林健康评价03-03
浙江乌岩岭昆虫及其森林健康评价03-03 -
 鸵蛾总科03-03鸵蛾总科,中形蛾子,翅宽,体粗壮。前翅常暗而后翅黑色,具黄或桔黄色的斑纹。有单眼,无毛隆。喙发达,下唇须前伸,喙状。本总科只有鸵蛾科 Hyblaeidae一科,已知2属18种。Hyblaea属17种分布于旧大陆的热带。
鸵蛾总科03-03鸵蛾总科,中形蛾子,翅宽,体粗壮。前翅常暗而后翅黑色,具黄或桔黄色的斑纹。有单眼,无毛隆。喙发达,下唇须前伸,喙状。本总科只有鸵蛾科 Hyblaeidae一科,已知2属18种。Hyblaea属17种分布于旧大陆的热带。 -

-
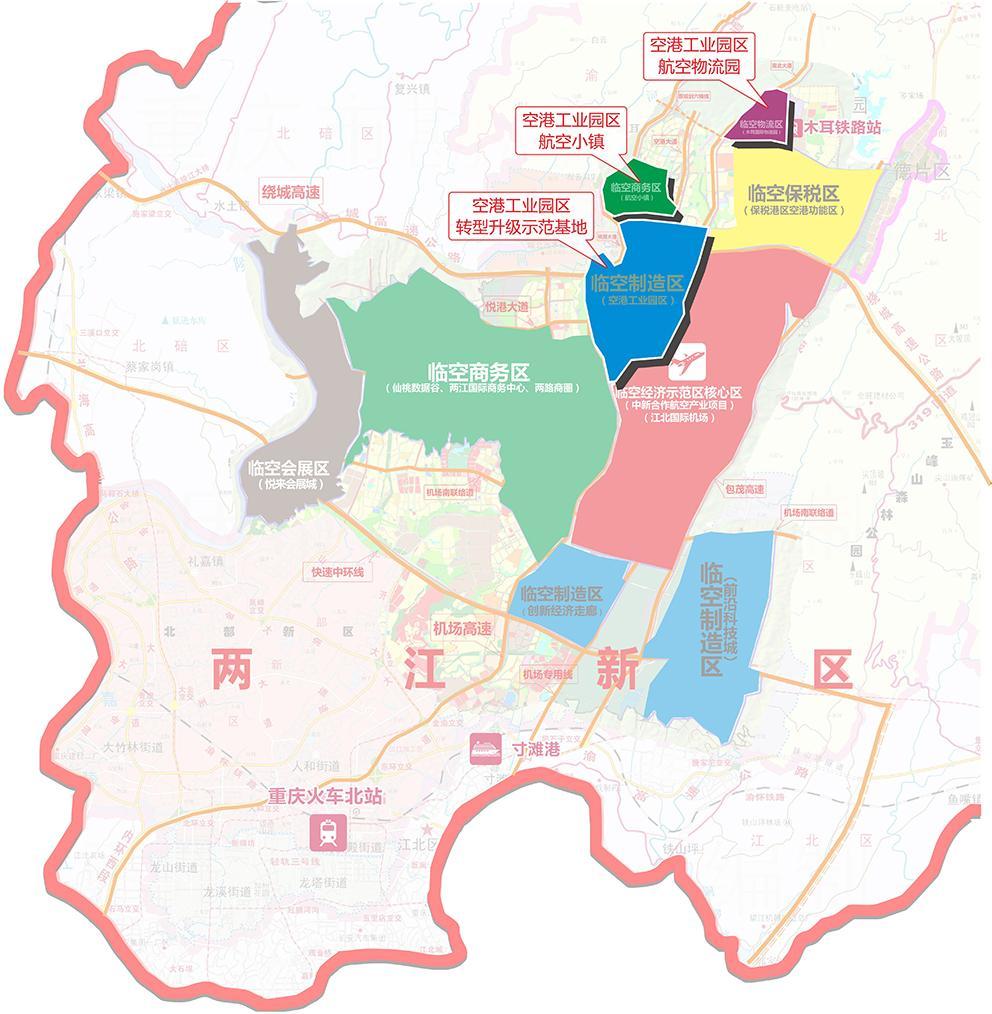 重庆空港工业园区03-03重庆空港工业园区于2002年1月正式动工建设;是市政府首批批准设立的市级特色工业园区,也是国家核准的省级开发(园)区、商务部确定的加工贸易梯度转移重点承接地和渝北建设“重庆对外开放第一门户”攻坚战的一大“战区”。
重庆空港工业园区03-03重庆空港工业园区于2002年1月正式动工建设;是市政府首批批准设立的市级特色工业园区,也是国家核准的省级开发(园)区、商务部确定的加工贸易梯度转移重点承接地和渝北建设“重庆对外开放第一门户”攻坚战的一大“战区”。 -

-

-
 ZECO ES5003-03
ZECO ES5003-03 -

-
 肉牛饲料03-03
肉牛饲料03-03 -

-
 在绝望中寻找希望03-03在荒凉的沙漠腹地,将军、作家、公务员、屠夫、律师和工程师先后迷了路,面临着死亡的威胁。六个人结伴而行,希望能彼此协助摆脱困境。最后,只有一个人走出了沙漠,其他人都长眠于黄沙之下。这个幸存者是谁?为什么只有他重获新生?一段生死未卜的死亡之旅,一个发人深省的人生寓言。
在绝望中寻找希望03-03在荒凉的沙漠腹地,将军、作家、公务员、屠夫、律师和工程师先后迷了路,面临着死亡的威胁。六个人结伴而行,希望能彼此协助摆脱困境。最后,只有一个人走出了沙漠,其他人都长眠于黄沙之下。这个幸存者是谁?为什么只有他重获新生?一段生死未卜的死亡之旅,一个发人深省的人生寓言。 -
 Copula函数03-03Copula函数描述的是变量间的相关性,实际上是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数,因此也有人将它称为连接函数。相关理论的提出可以追溯到1959年,SKlar通过定理形式将多元分布与Copula函数联系起来。20世纪90年代后期相关理论和方法在国外开始得到迅速发展并应用到金融,保险等领域的相关分析,投资组合分析和风险管理等多个方面。定义;(Nelsen.2006) N 元Copula函数是指具有以下性质的函数(下记为C):(1)定义域为[0,1]×[0,1]×。×[0,1] (共为
Copula函数03-03Copula函数描述的是变量间的相关性,实际上是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数,因此也有人将它称为连接函数。相关理论的提出可以追溯到1959年,SKlar通过定理形式将多元分布与Copula函数联系起来。20世纪90年代后期相关理论和方法在国外开始得到迅速发展并应用到金融,保险等领域的相关分析,投资组合分析和风险管理等多个方面。定义;(Nelsen.2006) N 元Copula函数是指具有以下性质的函数(下记为C):(1)定义域为[0,1]×[0,1]×。×[0,1] (共为 -
 褚树荣03-03褚树荣,出生于1961年11月14日,浙江省中学语文特级教师,宁波大学课程教学论专业硕士生导师,曾接受中学语文学科骨干教师国家级培训。在《语文学习》《中学语文教学通讯》《中学语文教学参考》等刊物发表文章 50 余篇。曾领衔主编《新课程名师创新教学行为访谈录》《假日活动教程丛书》《新课程语文教学设计》《古诗文阅读与拓展》《话题作文 T 型台》,独立编著《教室的革命:语文主题活动新探索》《高中阅读教例剖析与教案编制》《古诗文阅读新视点》等语文教育教学类图书。
褚树荣03-03褚树荣,出生于1961年11月14日,浙江省中学语文特级教师,宁波大学课程教学论专业硕士生导师,曾接受中学语文学科骨干教师国家级培训。在《语文学习》《中学语文教学通讯》《中学语文教学参考》等刊物发表文章 50 余篇。曾领衔主编《新课程名师创新教学行为访谈录》《假日活动教程丛书》《新课程语文教学设计》《古诗文阅读与拓展》《话题作文 T 型台》,独立编著《教室的革命:语文主题活动新探索》《高中阅读教例剖析与教案编制》《古诗文阅读新视点》等语文教育教学类图书。 -
 梁英03-03
梁英03-03 -

-
 惠州工业科技学校03-03惠州工业科技学校是一所公办全日制国家级重点中等职业学校。具有近40年的深厚工科文化渊源,丰富的文秘、经济类中专办学经验。学校位于风景秀丽的惠州西湖风景区菱湖畔丰山旁,占地面积70余亩,建筑面积近5万平方米。学科专业门类齐全的专业设置 学校设有电子工程系、机电工程系、汽车工程系、信息工程系、工艺美术系、管理工程系等6个工科和文科学系,20个专业30个方向供学生自由选读。2012年与惠州农业学校 重组为惠州工程技术学校,并于2017年升格为惠州工程职业学院。
惠州工业科技学校03-03惠州工业科技学校是一所公办全日制国家级重点中等职业学校。具有近40年的深厚工科文化渊源,丰富的文秘、经济类中专办学经验。学校位于风景秀丽的惠州西湖风景区菱湖畔丰山旁,占地面积70余亩,建筑面积近5万平方米。学科专业门类齐全的专业设置 学校设有电子工程系、机电工程系、汽车工程系、信息工程系、工艺美术系、管理工程系等6个工科和文科学系,20个专业30个方向供学生自由选读。2012年与惠州农业学校 重组为惠州工程技术学校,并于2017年升格为惠州工程职业学院。 -


