指数函数是重要的基本初等函数之一。一般地，y=a函数(a为常数且以a>0，a≠1)叫做指数函数，函数的定义域是 R 。  注意，在指数函数的定义表达式中，在a前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式，否则，就不是指数函数  。

中文名

指数函数

外文名

exponential function

定义

是重要的基本初等函数之一

一般式

y=a^x(a>0且a≠1) (x∈R)

函数性质

既不是奇函数，也不是偶函数

值域区间

（0，+∞）

定义域

x∈R

单调递减

0\u003ca\u003c1时

单调递增

a>1时

基本概念

7348次播放04:58高一数学学霸笔记：指数函数的概念3563次播放02:38高中最重要的函数，指数函数及其学习技巧！

细胞的分裂是一个很有趣的现象，新细胞产生的速度之快是十分惊人的。例如某种细胞在分裂时，1个分裂成2个，2个分裂成4个……第x次分裂得到新细胞数y与分裂次数x的函数关系式：

。

这个函数是幂的形式，且自变量为幂指数，我们下面来研究这样的函数。

一般地，函数

(a为常数且以

，

)叫做指数函数，函数的定义域是R。对于一切指数函数来讲，值域为

。

指数函数中

前面的系数为1。如：

都是指数函数；

不是指数函数。

数学术语

指数函数

是数学中重要的函数。应用到值e上的这个函数写为

。还可以等价地写为e，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828，还称为欧拉数。

当

时，指数函数对于x的负数值非常平坦，对于x的正数值迅速攀升，在 x等于0的时候，y等于1。当

时，指数函数对于x的负数值迅速攀升，对于x的正数值非常平坦，在x等于0的时候，y等于1。在x处的切线的斜率等于此处y的值乘上lna。即由导数知识得：

作为实数变量x的函数，

的图像总是正的(在x轴之上)并递增(从左向右看)。它永不触及x轴，尽管它可以无限程度地靠近x轴(所以，x轴是这个图像的水平渐近线。它的反函数是自然对数

，它定义在所有正数x上。

有时，尤其是在科学中，术语

指数函数

更一般性地用于形如

（k属于R）的函数，这里的 a 叫做“底数”，是不等于 1 的任何正实数。本文最初集中于带有底数为欧拉数e 的指数函数。

指数函数的一般形式为

(

且

) (

)，从上面我们关于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得

且

。

基本性质

1万次播放14:38【指数函数的性质】 高中数学 必修一 第二章 函数 17 #学浪计划#

如图所示为a的不同大小影响函数图形的情况。

在函数中可以看到

：

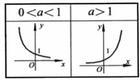
（1）指数函数的定义域为R，这里的前提是a大于0且不等于1。对于a不大于0的情况，则必然使得函数的定义域不连续，因此我们不予考虑，同时a等于0函数无意义一般也不考虑。

（2）指数函数的值域为

。

（3）函数图形都是上凹的。

（4）

时，则指数函数单调递增；若

，则为单调递减的。

（5）可以看到一个显然的规律，就是当a从0趋向于无穷大的过程中（不等于0）函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置，趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递增函数的位置。其中水平直线

是从递减到递增的一个过渡位置。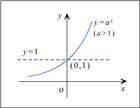

（6）函数总是在某一个方向上无限趋向于X轴，并且永不相交。

（7）函数总是通过（0，1）这点,(若

,则函数定过点

（8）指数函数无界。

（9）指数函数是非奇非偶函数

（10）指数函数具有反函数，其反函数是对数函数，它是一个多值函数。

运算法则

①

②

③

④

函数图像

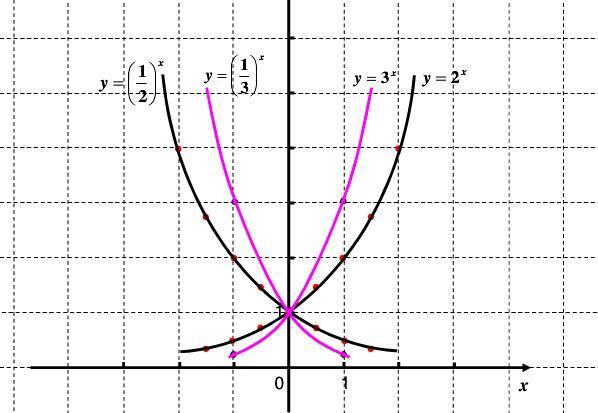
3930次播放02:35高一数学：指数函数的图象识别2400次播放02:49高一数学学霸笔记：指数函数的图象变换1728次播放02:23高一数学：指数函数图象关系的识别1108次播放02:00高一数学：指数函数图象的定点问题

(1)由指数函数

与直线x=1相交于点

可知：在y轴右侧，图像从下到上相应的底数由小变大。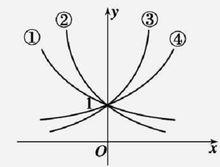

(2)由指数函数

与直线

相交于点

可知：在y轴左侧，图像从下到上相应的底数由大变小。

(3)指数函数的底数与图像间的关系可概括的记忆为：在y轴右边“

底大图高

”；在y轴左边“

底大图低

”。（如右图）。

(4)

与

的图像关于y轴对称。

幂的比较

比较大小常用方法：

（1）做差（

商）法

：

大于0即A大于B

等于0即

小于0即A小于B 步骤：做差—变形—定号—下结论；

大于1即A大于B

等于1即A等于B

小于1即A小于B （A，B大于0）

（2）函数单调性法；

（3）

中间值法

：要比较A与B的大小，先找一个中间值C，再比较A与C、B与C的大小，由不等式的传递性得到A与B之间的大小。

比较两个幂的大小时，除了上述一般方法之外，还应

注意

：

（1）对于底数相同，指数不同的两个幂的大小比较，可以利用

指数函数的单调性

来判断。

例如：

，

因为3大于1所以函数单调递增（即x的值越大，对应的y值越大），因为5大于4，所以y2 大于y1 。

（2）对于底数不同，指数相同的两个幂的大小比较，可

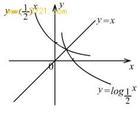
以利用

指数函数图像的变化规律

来判断。

例如：

,

,因为

小于1所以函数图像在定义域上单调递减；3大于1，所以函数图像在定义域上单调递增，在

是两个函数图像都过

然后随着x的增大，y1图像下降，而y2上升，在x等于4时，y2大于y1.

（3）对于底数不同，且指数也不同的幂的大小比较，则可以利用

中间值

来比较。如：

<1> 对于三个（或三个以上）的数的大小比较，则应该先根据值的大小（特别是与0、1的大小）进行

分组

，再比较各组数的大小即可。

<2> 在比较两个幂的大小时，如果能充分利用“1”来搭“桥”（即比较它们与“1”的大小），就可以快速地得到答案。那么如何判断一个幂与“1”大小呢？由指数函数的图像和性质可知“同大异小”。即当底数a和1与指数x与0之间的不等号同向（例如： a 〉1且

，或

〈 1且 x〈 0）时，

大于1，异向时

小于1。