人物生平

笛沙格
吉拉德·笛沙格
(Girard Desargues,1591年2月21日生于法国里昂,3月2日受洗,1661年10月卒于里昂),法国数学家和工程师,别名S.G.D.L. ,他署名Sieur Girard Desargues Lyonnois的缩写。射影几何的创始人之一,他奠定了射影几何的基础。以他命名的事物有笛沙格定理、笛沙格图、笛沙格平面,1964年,国际天文学联合会以他的名字命名一个月球环形山。他建立了统一的二次曲线理论,是笛沙格定理三角形的角度,也笛沙格定理的退化(参见南师大周兴和[高等几何]第四章,P.98,科学出版社,2003)。笛沙格出生于里昂的一个为法国王室服务的家庭。他的父亲是皇家公证人。笛沙格于1645开始建筑师生涯。在此之前,他是作为一名导师,可能是黎塞留的随行工程技术顾问。作为建筑师,他在巴黎和里昂设计了几个私人和公共建筑;作为工程师,他设计了一个安装在巴黎附近的提水系统,这个设计基于当时尚不了解的外摆线轮原理。
作为建筑师的笛沙格的数学著作早在1639年就已问世,其中已有笛沙格定理的描述,并已有了射影几何的雏形,不但没有引起较大关注,他的发现反而引起了当时数学界人士和宗教人士的一些不愉快。做为一名巧匠,他将他的投影透视技术教授给了一些人。他的定理从他去世后直到18世纪也没引起注意。1864年他的作品被重新发现和再版,随后被收集到L'oeuvre mathématique de Desargues一书中。在他的晚年,笛沙格公开了标有神秘标题“DALG”的文件,对这标题最普遍认可的看法是亨利·布罗卡提出的:Des Argues, Lyonnais, Géometre。
笛沙格定理
笛沙格
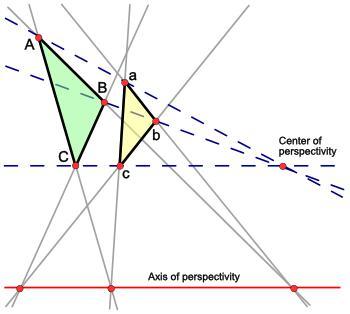
在射影几何,笛沙格定理作为一个古老而著名的定理,有着重要的应用。Desargues的定理,被以他的名字命名 以纪念Gérard Desargues。陈述如下:在一个射影空间,二个三角轴向地是在透视,如果,并且,只有当他们在透视在中心。
要了解此,由(小写) a表示一个三角三个端点、b和c,并且那些其他由(资本) A、B和C.轴向是在线满意的,如果和,只有当交点ab的与AB的和那ac的交叉点与AC的和那交叉点BC有BC的,是在同一直线上的,条件称轴。中央是条件满意,如果和,只有当三条线Aa, Bb和Cc是一致的,在称透视中心的点。
笛沙格定理:
笛沙格
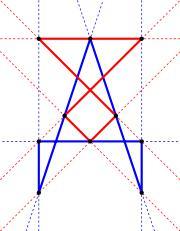
投影对仿射空间在仿射空间,只有当一个列出偶然地介入平行的线的各种各样的例外一个相似的声明是真实的。因此的笛沙格定理是一个自然家在投影而不是的最基本简单和直觉的几何定理仿射空间。
Desargues的定理真相在飞机的通过塑造它在三维的空间和随后射出结果欣然推论入飞机比通过实际修建在2空间的证明。除非他们适合入空间维度3或较少,二个三角不可能在透视; 因而在更高的维度二个三角的精炼间距总是维度子空间没有高于3。
Desargues的定理可以陈述如下:
如果A.a, B.b, C.c是一致的,然后
(A.B)∩ (a.b), (A.C) ∩ (a.c), (B.C)∩ (b.c)是在同一直线上的。
用纯粹符号术语,使用交叉产品和数量积, Desargues的定理可以陈述象如此:如果
(A \时期a) \ cdot (B \时期b) \时期(C \时期c) = 0
然后
((A \时期B) \时期(a \时期b)) \ cdot (((A \时期C) \ cdot (a \时期c)) \时期((B \时期C) \时期(b \时期c))) = 0。
让表示标量三重积, Desargues的定理可以因而陈述:如果
\ langle A \时期a, B \时期b, C \时期c \ rangle = 0
然后
\ langle (A \时期B) \时期(a \时期b), (A \时期C) \时期(a \时期c), (B \时期C) \时期(b \时期c) \ rangle = 0。
第一再声明
知道传染媒介三重积
x \时期(Y \时期Z)
是相等的
Y (X \ cdot Z) - Z (X \ cdot Y),
一可能获得惯例
(X \时期Y) \时期(Z \时期W) = \ langle x, Y, W \ rangle Z - \ langle x, Y, Z \ rangle W。
从最后惯例,一个可能进一步获得身分
\ langle U \时期v, W \时期x, Y \时期Z \ rangle = \ langle W, X, Z \ rangle \ langle U, V, Y \ rangle - \ langle W, X, Y \ rangle \ langle U, V, Z \ rangle。
通过这个身分的应用, Desargues的定理可以被再声明如下:
如果
\ langle B, b, c \ rangle \ langle A, a, C \ rangle = \ langle B, b, C \ rangle \ langle A, a, c \ rangle
然后
\ langle A \时期C, a \时期c, b \时期c \ rangle \ langle A \时期B, a \时期b, B \时期C \ rangle = \ langle A \时期C, a \时期c, B \时期C \ rangle \ langle A \时期B, a \时期b, b \时期c \ rangle。
第二再声明
再申请身分于Desargues的定理,通勤的三重积和周期交换每三重积传染媒介的第一再声明的结果,一个得到这第二再声明:
如果
\ langle A, a, c \ rangle \ langle b, B, C \ rangle = \ langle a, A, C \ rangle \ langle B, b, c \ rangle
然后
\ langle C, a, c \ rangle \ langle b, A, B \ rangle = \ langle c, A, C \ rangle \ langle B, a, b \ rangle。
注意结果的左边可以从前事的左边获得通过代替A→C, B→A, C→B。并且,结果的右边可以从前事想法的右边获得代替a→c, b→a, c→b。
第三再声明
传染媒介微积分定理阐明,二标量三重积产品与元素是规则取决于的数量积矩阵的定列式是相等的
M_ {ij} = u_i \ cdot v_j, \ qquad \ langle u_1, u_2, u_3 \ rangle \ langle v_1, v_2, v_3 \ rangle = |M|.
申请这个定理于第二再声明产生这第三个:
如果
\离开| \开始{矩阵} A \ cdot b & a \ cdot b & c \ cdot b \ \ A \ cdot B & a \ cdot B & c \ cdot B \ \ A \ cdot C & a \ cdot C & c \ cdot C \末端{矩阵} \正确| = \| \开始{矩阵} a \ cdot B & A \ cdot B & C \ cdot B \ \ a \ cdot b & A \ cdot b & C \ cdot b \ \ a \ cdot c & A \ cdot c & C \ cdot c \末端{矩阵} \正确|
然后
\离开| \开始{矩阵} C \ cdot b & a \ cdot b & c \ cdot b \ \ C \ cdot A & a \ cdot A & c \ cdot A \ \ C \ cdot B & a \ cdot B & c \ cdot B \末端{矩阵} \正确| = \| \开始{矩阵} c \ cdot B & A \ cdot B & C \ cdot B \ \ c \ cdot a & A \ cdot a & C \ cdot a \ \ c \ cdot b & A \ cdot b & C \ cdot b \末端{矩阵} \正确|.
第四再声明
扩展第三再声明的定列式产生第四这一个:
如果
(A \ cdot b) (a \ cdot B) (c \ cdot C) + (a \ cdot b) (c \ cdot B) (A \ cdot C) + (c \ cdot b) (A \ cdot B) (a \ cdot C)
- (A \ cdot b) (c \ cdot B) (a \ cdot C) - (a \ cdot b) (A \ cdot B) (c \ cdot C) - (c \ cdot b) (a \ cdot B) (A \ cdot C)
= (a \ cdot B) (A \ cdot b) (C \ cdot c) + (A \ cdot B) (C \ cdot b) (a \ cdot c) + (C \ cdot B) (a \ cdot b) (A \ cdot c)
- (a \ cdot B) (C \ cdot b) (A \ cdot c) - (A \ cdot B) (a \ cdot b) (C \ cdot c) - (C \ cdot B) (A \ cdot b) (a \ cdot c)
然后
(C \ cdot b) (a \ cdot A) (c \ cdot B) + (a \ cdot b) (c \ cdot A) (C \ cdot B) + (c \ cdot b) (C \ cdot A) (a \ cdot B)
- (C \ cdot b) (c \ cdot A) (a \ cdot B) - (a \ cdot b) (C \ cdot A) (c \ cdot B) - (c \ cdot b) (a \ cdot A) (C \ cdot B)
= (c \ cdot B) (A \ cdot a) (C \ cdot b) + (A \ cdot B) (C \ cdot a) (c \ cdot b) + (C \ cdot B) (c \ cdot a) (A \ cdot b)
- (c \ cdot B) (C \ cdot a) (A \ cdot b) - (A \ cdot B) (c \ cdot a) (C \ cdot b) - (C \ cdot B) (A \ cdot a) (c \ cdot b)。
第五再声明
两个等式的每边的第一个和第五个期限(前事和结果)第四再声明结束取消,产生这第五再声明:
如果
(A \ cdot C) (B \ cdot c) (a \ cdot b) + (A \ cdot B) (C \ cdot a) (b \ cdot c)
- (A \ cdot b) (B \ cdot c) (C \ cdot a) - (A \ cdot C) (B \ cdot a) (b \ cdot c)
= (A \ cdot B) (C \ cdot b) (a \ cdot c) + (A \ cdot c) (B \ cdot C) (a \ cdot b)
- (A \ cdot c) (B \ cdot a) (C \ cdot b) - (A \ cdot b) (B \ cdot C) (a \ cdot c)
然后
(A \ cdot c) (B \ cdot C) (a \ cdot b) + (A \ cdot C) (B \ cdot a) (b \ cdot c)
- (A \ cdot c) (B \ cdot a) (C \ cdot b) - (A \ cdot C) (B \ cdot c) (a \ cdot b)
= (A \ cdot B) (C \ cdot a) (b \ cdot c) + (A \ cdot b) (B \ cdot C) (a \ cdot c)
- (A \ cdot b) (B \ cdot c) (C \ cdot a) - (A \ cdot B) (C \ cdot b) (a \ cdot c)。
第六再声明
在第五再声明的二个等式之间有八个不同期限:两次出现的每一个。让期限relabeled如下:
t_1 = (A \ cdot C) (B \ cdot c) (a \ cdot b),
t_2 = (A \ cdot B) (C \ cdot a) (b \ cdot c),
t_3 = (A \ cdot b) (B \ cdot c) (C \ cdot a),
t_4 = (A \ cdot C) (B \ cdot a) (b \ cdot c),
t_5 = (A \ cdot B) (C \ cdot b) (a \ cdot c),
t_6 = (A \ cdot c) (B \ cdot C) (a \ cdot b),
t_7 = (A \ cdot c) (B \ cdot a) (C \ cdot b),
t_8 = (A \ cdot b) (B \ cdot C) (a \ cdot c)。
然后第五再声明成为下列:
如果
t1 + T2 − t3 − t4 = t5 + t6 − t7 − t8
然后
t6 + t4 − t7 − t1 = T2 + t8 − t3 − t5。
第七再声明
在第六再声明的前事的等式的右边移动期限向左边和期限在结果的等式的左边向右边。结果是:
如果
t1 + T2 − t3 − t4 − t5 − t6 + t7 + t8 = 0
然后
0 = t1 + T2 − t3 − t4 − t5 − t6 + t7 + t8。