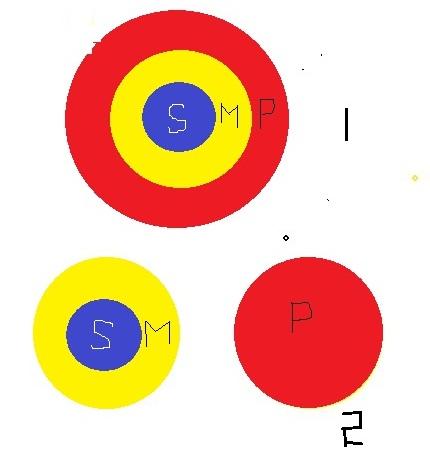
凡对全类有所肯定,则对全类的分子也有所肯定;凡对全类有所否定,则对全类的分子也有所否定。图2表示:s类包含于m类,m类与p类全异,所以,s类与p类全异。
三段论公理相关的文章
周伯通是是金庸所著武侠小说《射雕英雄传》和《神雕侠侣》中的人物,他天性纯真,爱捉弄别人,故有“老顽童”之称,在《射雕英雄传》第十六回首次出场,在小说中,周伯通为王重阳(书中为“天下五绝”之首,有“中神通”之号)的师弟,全真七子的师叔,是为全真教创始人之一。为金庸小说中武功绝顶的高手之一。
林朝英是金庸武侠小说《神雕侠侣》中的虚构人物,古墓派的开山祖师。她是小龙女的师祖,杨过的太师祖。林朝英的武功被认为是武林中最高的,超越了东邪、西毒、南帝和北丐等四大宗师。尽管她是一位女性,但由于不争名利,所以并没有很大的声望。林朝英与全真教的开山祖师王重阳是一对冤家情侣。她的容貌极美,但眼角间隐含着
玉山铁二(1980年4月7日出生于日本京都府城阳市)是一位日本影视男演员。他毕业于京都府立西城阳高中,并于1999年通过出演个人首部电视剧《麻辣女教师》正式进入演艺圈。2001年,他参演了特摄剧《百兽战队牙吠联者》。2004年,玉山铁二首次担任主演,出演运动电影《功夫棒球》,在片中饰演不屈斗志。20
香港天文台(简称天文台;英语:Hong Kong Observatory,简称HKO)是商务及经济发展局(前经济发展及劳工局)辖下的部门,也是世界气象组织成员,专责香港的气象观测、地震、授时、天文及辐射监测等工作,并向香港公众发出相关的警告。现任天文台台长为岑智明。
山西本词条是多义词,共3个义项中华人民共和国省级行政区山西,简称“晋”,中华人民共和国省级行政区,省会太原,位于中国华北,东与河北为邻,西与陕西相望,南与河南接壤,北与内蒙古毗连,介于北纬34°34′—40°44′,东经110°14′—114°33′之间,总面积15.67万平方千米。山西省地势呈东北斜向西南的平行四边形,是典型的为黄土覆盖的山地高原,地势东北高西南低。高原内部起伏不平,河谷纵横,地

尚可名片
这家伙太懒了,什么都没写!