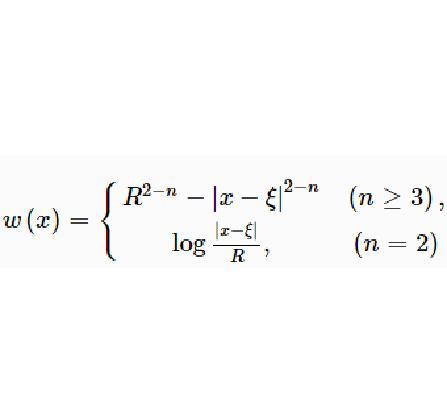闸函数(barrier function)是用来界定区域边界性状的一种函数。又称障碍函数。处理优化问题时，在极值点的搜索过程中，为保证搜索始终在可行域内，对企图从可行域内部穿越边界的点，在目标函数中加入障碍项，表示障碍项的函数即为闸函数。距边界越近，障碍越大，当趋于边界时，障碍趋于无穷大，从而保证最优解不会超出可行域。
精选百科
本文由作者推荐
闸函数
闸函数
外文名
barrier function
基本介绍
闸函数(barrier function)是用来界定区域边界性状的一种函数。设
1.
2.在
则称
正则边界点
1. 在
闸函数
，即存在
相关定理
定理1
设
定理2
设
的解存在。
由定理2 可知，求解Dirichlet问题就转化为当
闸函数相关的文章
小编整理：香港岛，香港特别行政区下辖行政区。香港岛（英文：HongKongIsland），简称为港岛，是中国香港最繁华的地方。香港岛简称为港岛香港岛（英文:HongKongIsland），简称为港岛，是香港最繁荣的地方。基本信息中文名香港岛外文名HongKon
木卫二（Europa，古希腊语：Ευρώπη），又称为欧罗巴，是木星的第六颗已知卫星，也是木星的第四大卫星。在1610年被伽利略发现后，木卫二由西门·马里乌斯独立发现。木卫二的公转轨道距离木星第五近，稍微比月球小。 木卫二是一个温和的世界，表面覆盖着冰层，底层是一片海洋。科学家认为，地球上海洋孕育了
馅饼是一种中国北方的家常食品，它由多层饼皮包裹着馅料制成。制作馅饼的方法包括煎、烤和焗等多种方式。馅料的种类繁多，包括肉类、蔬菜、海鲜和鸡蛋等，味道以咸鲜为主。 馅饼也被称为盒子，在中国台湾和大陆被译作派，在中国香港被译作批。这个名称源自英语单词"pie"。馅饼是一种烤焗食品，由饼皮包裹着馅料制成。
亚得里亚海，意大利语作Mare Adriatico，英语作Adriatic sea。地中海的一个大海湾。长约800公里(500哩)，平均宽160公里(100哩)，平均水深444公尺(1,457呎)，最深处1,324公尺(4,035呎)，面积131,050平方公里(50,590平方哩)。北浅、南深，平
汉军是汉王朝的军队，秦二世元年（公元前209年），汉高祖刘邦在沛县带领3000人起义，这是汉军的前身，汉元年（公元前206年），在诸侯推翻秦朝后，刘邦被项羽封为汉王，之后，刘邦带领的军队被称为汉军。
高僧高僧：宋代文物陶模高僧宋代（960年—1279年）开封基本信息出土地点东京所属年代宋代基本信息【藏品名称】：高僧【藏品现状】：开封大学大观博物馆收藏藏品介绍高僧宋代（960年—1279年）开封HierarchSongDynasty(960–1279A.D.
尚可名片
这家伙太懒了，什么都没写！
作者
