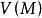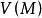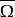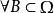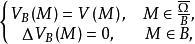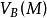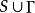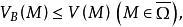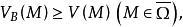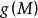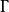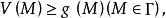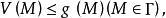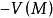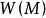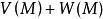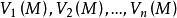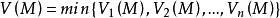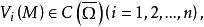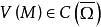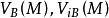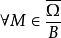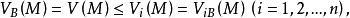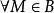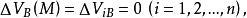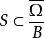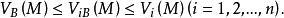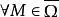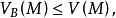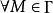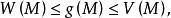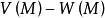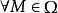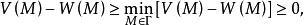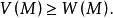下调和函数(subharmonic function)亦称次调和函数,是亚调和函数的一个子类。若-f为上调和函数,则f称为同一区域内的下调和函数,此时,若φ(t)是t的单调增的凸函数,则φ°f为下调和函数。例如,当u(x)为D⊂R上的复值解析函数,实数α>0时,|u(x)|与αlog|u(x)|都是下调和函数。
精选百科
本文由作者推荐
下调和函数相关的文章
郭靖,是金庸武侠小说《射雕英雄传》男主角和《神雕侠侣》中的重要角色,《倚天屠龙记》中也曾引述其相关事迹,他是贯通"射雕三部曲"的关键人物之一。融合“降龙十八掌”、“九阴真经”和“左右互搏”三大盖世武功为一体,遂翩然翱翔,武林尊为“天下第一侠士”,黑白二道俯首称臣,号令武林群雄,率领群雄守护着南宋襄阳
沙特阿拉伯王国(阿拉伯语:مملكةعربيةسعودية,英语:Kingdom of Saudi Arabia),通称沙特阿拉伯(Saudi Arabia),简称沙特。沙特位于阿拉伯半岛。东濒波斯湾,西临红海,同约旦、伊拉克、科威特、阿联酋、阿曼、也门等国接壤,并经法赫德国王大桥与巴林相接。海岸线
大流士一世(Darius I)(约公元前550年—约公元前486年),波斯帝国第三位皇帝,曾跟随皇帝冈比西斯二世远征埃及,冈比西斯二世逝世后,夺取皇位,登基称帝。大流士一世在位期间,在国内实行改革,推行行省制、统一货币、建设驿道,促进了波斯帝国的经济文化发展;对外则大举用兵,先后攻下印度河流域、埃及
库车站位于中国新疆维吾尔自治区阿克苏地区,是中国铁路乌鲁木齐局集团有限公司管辖的三等站,建于1998年,建筑面积1818㎡。库车站为库车地区铁路主要客货运站,车站主要办理衔接方向旅客列车的通过作业,以及库车至阿克苏、库尔勒方向区段,摘挂列车的解编作业。

尚可名片
这家伙太懒了,什么都没写!
作者