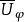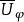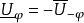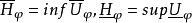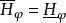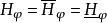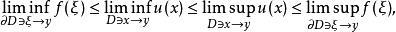可解集(resolutive set)是使其上-广义狄利克雷问题可解的MP集。
精选百科
本文由作者推荐
可解集相关的文章
营养不良是指体内营养素失衡所引起的消化系统疾病,包括营养不足和营养过剩,临床中多以营养不足为主,多由于良性疾病所致,近年来由恶性肿瘤所引起的营养不足人群也逐年增加。营养不良在世界各地,男女老少都可发生,但以婴幼儿和老人为多见。营养不良依据发病机制可分为原发性和继发性。原发性营养不良主要由于食物中蛋白
孙婆婆是金庸小说《神雕侠侣》中的人物。她是古墓派的奴仆,将小龙女养大,并略懂古墓派武功,这些武功是她从林朝英的丫鬟那里学来的。孙婆婆因为救杨过而死于全真道士郝大通之手。在临死前,她请求小龙女收留杨过,并将杨过托付给小龙女照顾。孙婆婆的来历不详,她一直是林朝英的弟子,直到她去世后与小龙女相依为命。她有
小编整理:欧麦尔二世是阿拉伯帝国伍麦叶王朝的第八任哈里发,他在位时间为717年至720年。欧麦尔二世是阿卜杜勒·阿齐兹的儿子,他的全名为欧麦尔·本·阿卜杜勒·阿齐兹·本·麦尔旺·本·哈凯姆。欧麦尔二世生于埃及的赫勒万,他在其父的熏陶下自幼能背诵《古兰经》,并初

尚可名片
这家伙太懒了,什么都没写!
作者