等距曲面（等距曲面）

内容概念

等距曲面指在罗氏空间中，在给定平面α的同一侧，到α的距离相等的点的轨迹。平面α称为等距曲面的底，从曲面上的任一点所引的到底上的垂线称为高。等距面是双曲线把的直交曲面。它也可以看成等距线绕双曲线束中的任一条直线旋转而生成的曲面。

罗氏几何

罗巴切夫斯基几何的简称。非欧几何的一种，亦称“双曲几何学”。是俄国数学家罗巴切夫斯基创立的。罗氏几何的创立是从研究“欧氏几何”第5公设即著名的平行公理(见“欧几里德几何”)是否能用其他公理证明开始的。平行公理不仅在形式上比其他公设复杂，而且在《几何原本》中，从第29个命题开始才用到这个公理，于是人们产生了能否把它作为定理而从其他公设和基本概念导出来的愿望。从古代开始，很多数学家企图证明第5公设，但经历了两千多年的时间都未成功。直到1826年，喀山大学的数学教授罗巴切夫斯基才彻底解决了这一问题，他于同年2月23日，在物理数学系的会议上宣读了《关于几何原理的议论》，这篇报告在1829年刊登在喀山大学学报上。

罗巴切夫斯基早在1815年就开始研究第五公设，最初他企图用反证法证明第5公设，但是，从与欧氏平行公理相矛盾的命题出发，展开推论，虽然得出一些在当时看来是不可思议的结果，却始终没有发现逻辑上的矛盾，罗巴切夫斯基由此得出两个结论：①平行公理不能被证明;②新的与欧氏几何对立的几何学本身无矛盾，在逻辑上是可能成立的。并于1835年出版专著《新几何原本》，后人称之为罗巴切夫斯基几何学，简称“罗氏几何”。

罗氏几何引用了与平行公理相反的公理：“过直线外一点至少可以作两条直线和已知直线不相交。”同时证明三角形三内角之和小于

基本曲面

罗氏空间的基本曲面是罗氏几何的主要研究对象。指罗氏空间中球面、等距曲面和极限球面三种曲面，这三种曲面分别是罗氏空间中三种线把——椭圆线把、双曲线把和抛物线把的直交曲面。如果以椭圆、双曲、抛物三种线束中的任一条直线为旋转轴，把圆、等距线、极限圆旋转，就分别得到罗氏空间中的三种回转曲面：球面、等距曲面，及极限球面。

球面介绍

罗氏空间的球面是罗氏空间的三种基本曲面之一。在罗氏空间中，设

直线把类型

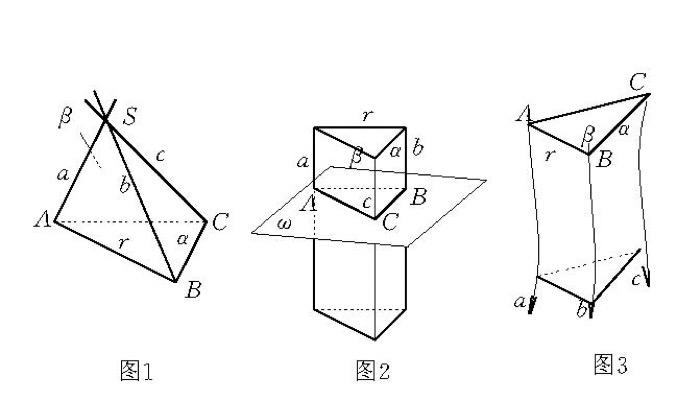
罗氏空间中的直线把是罗氏几何研究的对象。指罗氏空间中的直线集合，其中每对直线在一平面上。罗氏空间中的直线把只存在如下三种类型：

椭圆线把

2.双曲线把。垂直于某平面ω的所有直线的集合(如图2)。

3.抛物线把。在一方向相互平行的所有直线的集合(如图3)。

极限球面

罗氏空间的极限球面是罗氏空间的三种基本曲面之一。指在罗氏空间中，从直线a的一个点A，到在确定方向上与a平行的任意直线引等倾割线，其端点的几何轨迹。点A也是极限球面上的点。直线a及与a在同方向平行的直线称为极限球面的轴线。极限球面是抛物线把的直交曲面，也是极限圆绕其任一轴线旋转一周所产生的曲面。

人物简介

俄国数学家。生于下诺夫哥罗德(今高尔基城)，卒于喀山。1807年入喀山大学学习，1811年获硕士学位并留校工作。1816年任副教授，1822年任教授。还曾任物理数学系主任、图书馆馆长和喀山大学校长等职。罗巴切夫斯基是非欧几里得几何学的创始人之一。他从1816年开始试作平行公设(欧几里得《几何原本》中的第五公设)的证明。他把全部几何命题按是否依赖于平行公设而分为两部分，不靠平行公设的那部分现通称为“绝对几何学”。他从绝对几何中的命题“在一个平面上，过直线AB外一点至少可作一条直线与AB不相交”出发，在严密的推导下得到一系列前后一贯的命题，由此构成了逻辑上无矛盾且与绝对几何不相冲突，但又与欧几里得几何不同的新几何体系。罗巴切夫斯基称之为“虚几何学”，后人则称之为“罗巴切夫斯基几何学”。1826年，他在喀山大学公开发表自己的新学说，但没有得到承认。以后他陆续用俄文、法文、德文发表自己的工作。他去世后，高斯对他的学说予以肯定，他的工作逐渐引起人们重视。直到1868年，意大利数学家贝尔特拉米发表著名的论文，给出罗巴切夫斯基几何学的直观解释，他的发现才最终得到确认。除此之外，罗巴切夫斯基在无穷级数论、积分学和概率论等方面，也有出色的工作。他还是一位杰出的教育家和管理者，创立了喀山数学学派和喀山数学教育学派。其代表作有《具有完善的平行线理论的新几何学原理》、《论几何学基础》(1829—1830)、《平行线理论的几何研究》(1840，德文)等。