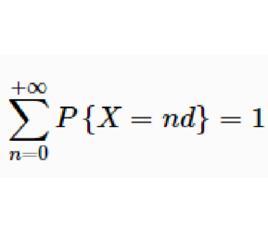格点分布亦称算术分布,是指一类离散型概率分布。称随机变量服从算术分布,如果其一切可能值构成(有限或无限)等差数列,即其一切可能值可以表示为a±md(m=0,1,2,…)的形式,其中a和d为常数;d称做分布的“步长”。二项分布、负二项分布、超几何分布、负超几何分布、泊松分布……以及许多常用离散分布都是算术分布。
精选百科
本文由作者推荐
格点分布相关的文章
小编整理:陈红是陈凯歌的妻子,她也是圈内流量小生陈飞宇的母亲。陈红是一位优秀的制片人和合作伙伴,对陈凯歌的事业和家庭生活都起到了重要的作用。在电影《长津湖》中,她担任制片人,与导演陈凯歌一起工作,这部电影的成功也离不开他们的通力合作。陈红出生于军人世家,从小就
黑海(英文名:Black Sea;俄文名:Чёрное море)是亚欧大陆西南部内陆海,北部与乌克兰接壤,东北部与俄罗斯接壤,东部与格鲁吉亚接壤,南部与土耳其接壤,西部与保加利亚和罗马尼亚接壤,经纬度范围为北纬46°33'至40°56,东经27°27'至41°42',面积约42.2万平方千米,平均
伊朗伊斯兰共和国(波斯语:جمهوریاسلامیایران,英语:The Islamic Republic of Iran,Iran),简称“伊朗”,位于西亚,属中东国家,东邻巴基斯坦和阿富汗,与土库曼斯坦接壤,西北与阿塞拜疆和亚美尼亚为邻,西接土耳其和伊拉克,中北部紧靠里海、南靠波斯湾和阿拉伯海

尚可名片
这家伙太懒了,什么都没写!
作者