零向量（数学术语之一）

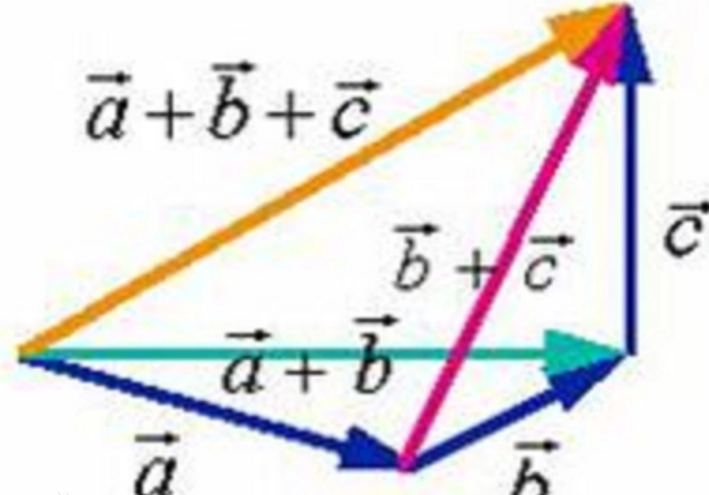
定义

mod（模）等于零的向量叫做零向量，记作0。

向量

在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的只有大小，没有方向的量叫做数量（物理学中称标量）。

向量的记法：印刷体记作粗体的字母（如a、b、u、v），书写时在字母顶上加一小箭头“→”。如果给定向量的起点（A）和终点（B），可将向量记作AB（并于顶上加→）。在空间直角坐标系中，也能把向量以数对形式表示，例如Oxy平面中(2,3)是一向量。

在物理学和工程学中，几何向量更常被称为矢量。许多物理量都是矢量，比如一个物体的位移，球撞向墙而对其施加的力等等。与之相对的是标量，即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系，例如向量是对应于物理中的势能。

几何向量的概念在线性代数中经由抽象化，得到更一般的向量概念。此处向量定义为向量空间的元素，要注意这些抽象意义上的向量不一定以数对表示，大小和方向的概念亦不一定适用。因此，平日阅读时需按照语境来区分文中所说的"向量"是哪一种概念。不过，依然可以找出一个向量空间的基来设置坐标系，也可以透过选取恰当的定义，在向量空间上界定范数和内积，这允许我们把抽象意义上的向量类比为具体的几何向量。

性质

注意零向量的方向是无法确定的。但我们规定：零向量的方向与任一向量平行，与任意向量共线，与任意向量垂直。

零向量的方向不确定，但模的大小确定。但是注意向量与向量不能比较大小。例如，若向量a的模大于零，则向量a大于零向量的说法是错误的，因为实数之间可用比较大小，而向量之间不能比较大小。

零向量与任意向量的数量积为0。

思考与探究

（1）零向量的方向不是任意的，而是无法确定的

我们知道既有大小，又有方向的量叫做向量，而零向量概念只规定其大小为0，并没有谈及方向问题，那么零向量的方向到底怎样呢?按照向量的概念，零向量也是有方向的。由于受到有些教辅书的误导，不少的老师和学生都认为“零向量的方向是任意的”，我想这种说法的根据可能就是“零向量与任意向量平行”的规定，但是，李文明  认为这种说法是错误的，因为两个非零向量平行是指同向或反向的两个向量，“零向量与任意向量平行”的这种规定，并没有规定零向量方向如何。当规定中的任意向量是非零向量，我们也不能认为零向量的方向与这个非零向量的方向相同或相反;当规定中的任意向量是零向量，我们更是无法确定两个零向量的方向。由此可见，零向量的方向应该是“不确定的”，或者说是无法确定的，也就是说给我们一个零向量，没有人能够指出它的方向。换句话说零向量(起点与终点重合的向量)是退化的向量，它已经退化到只能确定其大小，而无法确定其方向的一类特殊向量。

（2）零向量与任意向量都是平行的

这是平行向量概念中的明确规定，也就是说零向量与任意向量都是共线的;这种规定使得任意两个平面向量的位置关系只有两种:共线或不共线，二者必居其一，也就是说平面向量可以分为两类:一类是共线向量，一类是不共线向量;不共线的两个向量一定是两个非零向量。 

例题

例1，判断下列命题的真假

（1）a·b=a·c可以推出a=0或b=c

（2）a·（b·c）-（a·b）·c=0

（1）假

（2）假

例2，与a平行的单位向量的个数有：

答当a不是零向量时，有两个；当a是零向量是有无数个。所以答案是两个或无数个。

关于垂直问题

零向量是否可以与其它向量垂直？

人教A版必修4对零向量垂直问题采取了回避的态度。

人们的探讨主要有以下三种观点。

1.肯定“零向量与任一向量垂直”的主要有以下一些观点：

（1）零向量平行于任何向量，那么零向量也平行于向量ａ的法向量，于是零向量垂直于向量ａ．否定了零向量与任一向量垂直，就是否定了零向量与任一向量平行．

（2）零向量在几何中的意义退化为一个点，点既然与线段平行，点同样也垂直于线段．

（3）两者没有本质性的对立，高等数学中一般认为0与任一向量垂直．为了与大学接轨，0可以与任一向量垂直．

2.持否定态度的观点主要有：

（1）不能与任意向量垂直．由于0方向的任意性，如果与某一向量的夹角为90°，那么也可以为任意度数．

（2）中学课本规定了零向量与任意向量平行，就相当于把零向量与任意向量的关系的唯一性确定了，无须再谈垂直的情况．

（3）与向量共线定理相矛盾．平面向量共线定理：向量ａ（ａ≠0）与ｂ共线，当且仅当有唯一一个实数λ，使ｂ＝λａ．现在令λ＝0，那么ｂ＝0，因为0可以和向量ａ垂直，所以ｂ不一定平行于ａ．

（4）忠于课本．（尽管仅仅是为了忠于教材这个理由有点牵强，但这却是很多人做出选择的主要理由．这也从一个侧面反映出作为权威媒介的教材的重要性．）

（以上内容摘自由一道高考题引发“零向量垂直问题”的探讨湖北武汉华中师范大学数学与统计学学院胡婷婷）

3.关注本质，应把精力集中在核心的、更重要的内容上。

（1）零向量的核心意义，就像实数集中的0在运算中的地位一样由于零向量的位置特殊，数学家们约定“零向

量的方向不确定”.这样，在处理问题时，可根据需要让零向量与某一向量平行或垂直。这是一种人为的、合乎习惯的并是方便于应用的规定，就像“0既不是正数，也不是负数”(其实也可说成“0既是正数，也是负数”)的作用一样.

（2）向量有它的几何原型—有向线段，而且我们借助于几何图形，用“三角形法则”等定义它的运算，因此“向量集数与形于一身”.如果从几何角度看向量的运算和运算律的意义，就有了解决几何问题的向量法，而且向量法的力量无限。这种力量集中体现在它仅用“向量相加的首尾相接法则”、“向量数乘的意义和运算律”、“向量数量积的意义和运算律”、“平面向量基本定理”等四条基本法则来解决几何问题。这些是中学向量教学应关注的核心问题。把精力集中在核心知识的研究上。

(以上引自把精力集中在核心知识的研究上的中小学数学（高中）2010.9）

零向量

运算规律

1.a+o=a

2.a-o=a

3.a·o=o·a=o(a为非向量)

4.a+（-a）=0