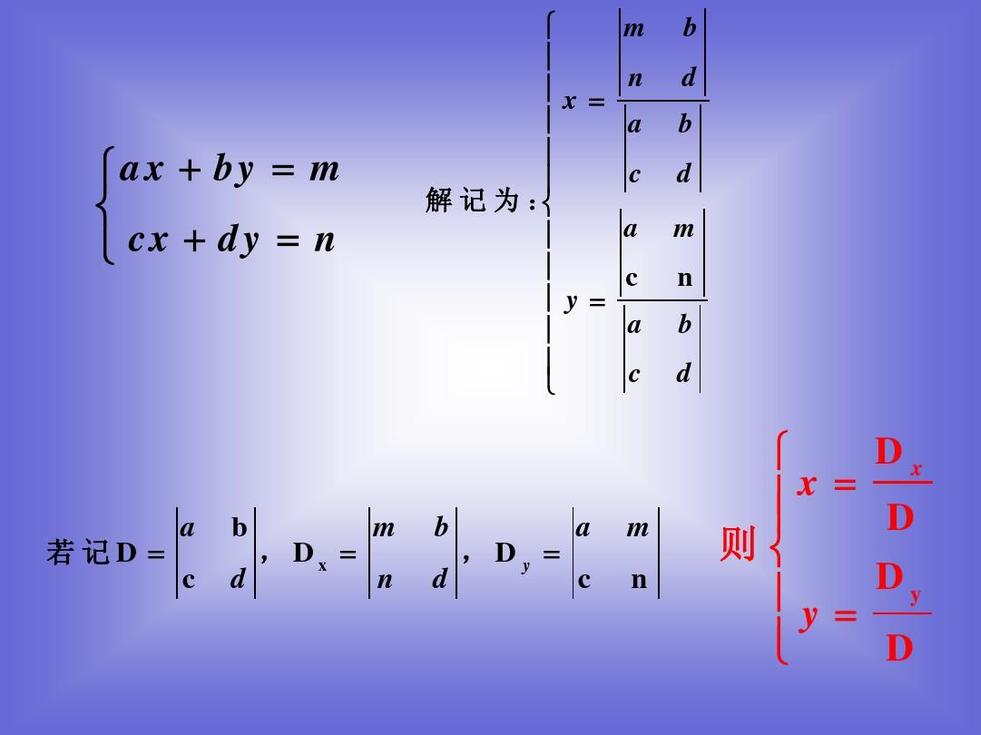
矩阵行列式是指矩阵的全部元素构成的行列式,设A=(aij)是数域P上的一个n阶矩阵,则所有A=(aij)中的元素组成的行列式称为矩阵A的行列式,记为|A|或det(A)。
精选百科
本文由作者推荐
矩阵行列式相关的文章
脑动脉瘤是常见血管性疾病,是自发性蛛网膜下腔出血最常见的原因。脑动脉瘤可见于任何年龄,但50~69岁患者居多,约占总发病率的2/3。动脉瘤病因不明,其发生是多种因素、多种机制并存导致。未破裂动脉瘤可无症状,较大的动脉瘤可压迫邻近脑组织或脑神经出现相应的局灶症状,如癫痫、偏瘫、失语、视力和视野障碍等。
阿卜杜拉·阿齐兹·伊本·沙特是阿卜杜·拉赫曼的儿子,出生于1880年,从小在科威特长大。1902年在科威特酋长穆巴拉克·萨巴赫的支持下,21岁的阿齐兹带领40多个勇士,骑着骆驼,向利雅得发起进攻,夺回利雅得,建立第三个沙特酋长国。
拉斯维加斯(LasVegas)是美国内华达州最大的城市,也是座享有极高国际声誉的城市。拉斯维加斯建市于1905年5月15日,因位于内华达州的沙漠边缘、边境,所以拉斯维加斯全年高温。
小编整理:库尔勒香梨是一种属于蔷薇科梨属植物的果实,它生长在天山高山上的野杜梨籽育苗作为砧木,具有抗寒、抗旱、抗病虫害的优势。它的特点包括皮薄、果心中大、果肉白色、肉质细腻酥脆、汁多味甜、近核部微酸,完熟后有香味、可溶性固型物含量11-14%,品质极上。库尔勒
生产建设兵团是指新中国成立后陆续组建的各类生产建设兵团,是中国通过军垦这种特殊体制达到巩固边防,发展经济,安置人员的目的,兵团成为党、政、军权合一,工、农、兵、学、商五位一体的半军事化组织和社会经济体系,尽管如今只有新疆生产建设兵团存在,但是在那段激情燃烧的岁月里,全国却陆续出现过12个兵团,3个农

尚可名片
这家伙太懒了,什么都没写!
作者